题目内容
5.在直角坐标系中,直线l1经过点(1,-3)和(3,1),直线l2经过(1,0),且与直线l1交于点A(2,a).(1)求a的值;
(2)A(2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点B,直线l2与y轴交于点C,求△ABC的面积.
分析 (1)首先利用待定系数法求得直线l1的解析式,然后直接把A点坐标代入可求出a的值;
(2)利用待定系数法确定l2的解析式,由于A(2,a)是l1与l2的交点,所以点A(2,a)可以看作是二元一次方程组$\left\{\begin{array}{l}{2x-y=5}\\{x+y=1}\end{array}\right.$的解;
(3)先确定B、C两点坐标,然后根据三角形面积公式计算.
解答 解:(1)设直线l1的解析式为y=kx+b,
把(1,-3)和(3,1)代入,
得$\left\{\begin{array}{l}{k+b=-3}\\{3k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-5}\end{array}\right.$,
则直线l1的解析式为:y=2x-5,
把A(2,a)代入y=2x-5,得:a=2×2-5=-1;
(2)设l2的解析式为y=mx+n,
把A(2,-1)、(1,0)代入,
得$\left\{\begin{array}{l}{2m+n=-1}\\{m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=1}\end{array}\right.$,
所以L2的解析式为y=-x+1,
所以点A(2,a)可以看作是二元一次方程组$\left\{\begin{array}{l}{2x-y=5}\\{x+y=1}\end{array}\right.$的解;
(3)把x=0代入y=2x-5,得y=-5,
把x=0代入y=-x+1,得y=1,
∴点B的坐标为(0,-5),点C的坐标为(0,1),
∴BC=1-(-5)=6.
又∵A点坐标为(2,-1),
∴S△ABC=$\frac{1}{2}$×6×2=6.
点评 本题考查了一次函数与一元一次方程的关系:由于任何一元一次方程都可以转化为ax+b=0(a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值,从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.

 口算能手系列答案
口算能手系列答案问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
| 品名次数 | 甲 | 乙 | 丙 | 丁 | 用钱金额(元) |
| 第一次购买件数 | 5 | 4 | 3 | 1 | 1882 |
| 第二次购买件数 | 9 | 7 | 5 | 1 | 2764 |
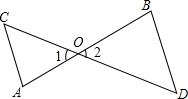 如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.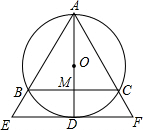 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.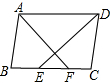 如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G
如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G