题目内容
10.已知三角形的周长小于13,各边长均为整数且三边各不相等,那么这样的三角形个数共有( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先根据三角形的两边之和大于第三边以及三角形的周长,得到三角形的三边都不能大于6.5;再结合三角形的两边之差小于第三边进行分析出所有符合条件的整数.
解答 解:根据三角形的两边之和大于第三边以及三角形的周长小于13,则其中的任何一边不能超过6.5;
再根据两边之差小于第三边,则这样的三角形共有3,4,2;4,5,2;3,4,5三个.
故选B.
点评 本题考查三角形的三边关系,且涉及分类讨论的思想.解答的关键是找到三边的取值范围及对三角形三边的理解把握.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.在解分式方程$\frac{1}{x-1}$+$\frac{x}{x-1}$=2时,我们第一步通常是去分母,即方程两边同乘以最简公分母(x-1),把分式方程变形为整式方程求解.解决这个问题的方法用到的数学思想是( )
| A. | 数形结合 | B. | 转化思想 | C. | 模型思想 | D. | 特殊到一般 |
18.在-2、-$\sqrt{2}$、0、1这四个数中,最大的数是( )
| A. | -2 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
15.阅读下列材料:
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
那么,购买每种体育用品各一件共需多少元?
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
| 品名次数 | 甲 | 乙 | 丙 | 丁 | 用钱金额(元) |
| 第一次购买件数 | 5 | 4 | 3 | 1 | 1882 |
| 第二次购买件数 | 9 | 7 | 5 | 1 | 2764 |
2.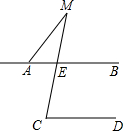 如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
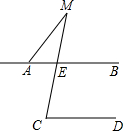 如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )| A. | 52° | B. | 42° | C. | 10° | D. | 40° |
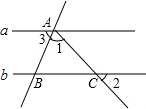 如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°.
如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°. 如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′.
如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′.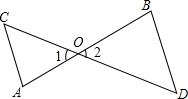 如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.