题目内容
3. 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.(1)∠F=30°,BC=2$\sqrt{3}$,求DF的长度;
(2)求证:BC=EC.
分析 (1)由正方形的性质可知∠BCF=90°,由∠F=30°,BC=2$\sqrt{3}$结合三角函数可求得CF的长,再由线段间的关系可得出结论;
(2)构造辅助线充分利用BM=CF-DN这个条件是关键,然后利用等角对等边的性质去证明.
解答 解:(1)∵四边形ABCD为正方形,
∴AD∥BC,∠BCF=90°,
∴CF=BC•cot∠F=2$\sqrt{3}$×$\sqrt{3}$=6,
∴DF=6-2$\sqrt{3}$.
(2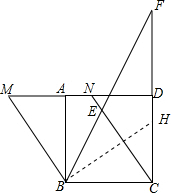 )在CD上截取CH=ND,如图,则可证Rt△BCH≌Rt△CDN
)在CD上截取CH=ND,如图,则可证Rt△BCH≌Rt△CDN
∴BH=CN=BM,∠HBC=∠NCD,
又HF=CF-CH=CF-DN=BM,
∴BH=FH
∴∠FBH=∠BFH
故∠FBC=∠FBH+∠HBC=∠BFH+∠NCD=∠BEC
∴BC=EC.
点评 本题考查了正方形的性质、勾股定理、平行四边形的判定及性质以及特殊角的三角函数值,解题的关键:(1)利用特殊角的三角函数值;(2)找到∠BEC=∠EBC.本题属于中档题,(1)没有难度,(2)稍微有点难度,解决该类型的题时,找边相等要想到两边所在的三角形为等边或者等腰三角形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
8.已知等边△ABC的边长为4,P是△ABC内一点,且点P在BC的垂直平分线上,若PA=$\sqrt{3}$,则PB长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
12. 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
 如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )
如图是两块完全一样的含30°角的三角板,分别记作△ABC和△A1B1C1,现将两块三角板重叠在一起,高较长直角边的中点为M,绕中点M转动上面的三角板ABC,直角顶点C恰好落在三角板△A1B1C1的斜边A1B1上.当∠A=30°,B1C=2时,则此时AB的长为( )
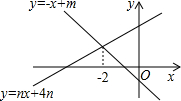 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )
如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )