题目内容
6.仔细观察式子,我们可作如下猜想:$\frac{a^3+b^3}{a^3+(a-b)^3}$=$\frac{a+b}{a+(a-b)}$.你能说明猜想是正确的吗?[友情提示:a3+b3=(a+b)(a2-ab+b2)].分析 利用a3+b3=(a+b)(a2-ab+b2)把分子分母因式分解,然后约分即可.
解答 解:$\frac{a^3+b^3}{a^3+(a-b)^3}$=$\frac{(a+b)({a}^{2}-ab+{b}^{2})}{[a+(a-b)][{a}^{2}-a(a-b)+(a-b)^{2}]}$=$\frac{(a+b)({a}^{2}-ab+{b}^{2})}{(a+a-b)({a}^{2}-ab+{b}^{2})}$=$\frac{a+b}{a+(a-b)}$.
所以猜想是正确的.
点评 本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 有些有理数不能在数轴上表示出来 | |
| B. | 对于两个数,较大数的相反数也较大 | |
| C. | 互为相反数的两个数的同一偶次数幂相等 | |
| D. | 一个数的相反数是非负数,则这个数一定是负数 |
11.下列各式x2+2x-3,x2-4x+3,x2+5x-6的公因式是( )
| A. | x-3 | B. | 3-x | C. | x+1 | D. | x-1 |
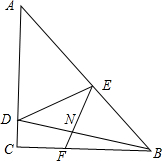 如图,在Rt△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,在AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD于点N.交BC于点F,若CF=8,AD=11,则CD的长为3.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,在AC上取一点D,在AB上取一点E,使∠BDC=∠EDA,过点E作EF⊥BD于点N.交BC于点F,若CF=8,AD=11,则CD的长为3. 如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数.
如图,在四边形ABCD中,AO是∠DAB的平分线,BO是∠ABC的平分线,AO与BO交于点O.若∠C+∠D=120°,求∠AOB的度数. 如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.
如图,正方形ABCD中,点M为DA延长线上一点,连接BM,过点C作CN∥BM,交AD于点N,在CD延长线上取一点F,使BM=CF-DN,连接BF,交CN于点E.