题目内容
7．已知一元二次方程2x2-5x+1=0的两个根为x1，x2，下列结论正确的是（ ）| A． | x1+x2=-$\frac{5}{2}$ | B． | x1•x2=1 | C． | x1，x2都是有理数 | D． | x1，x2都是正数 |
分析 先利用根与系数的关系得到x1+x2=$\frac{5}{2}$＞0，x1x2=$\frac{1}{2}$＞0，然后利用有理数的性质可判定两根的符号．
解答 解：根据题意得x1+x2=$\frac{5}{2}$＞0，x1x2=$\frac{1}{2}$＞0，
所以x1＞0，x2＞0．
∵x=$\frac{5±\sqrt{17}}{4}$，故C选项错误，
故选D．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
17．用反证法证明：在四边形中，至少有一个内角大于或等于90°，应先假设（ ）
| A． | 四边形中每一个内角都小于90° | |
| B． | 四边形中最多有一个内角不小于90° | |
| C． | 四边形中每一个内角都大于90° | |
| D． | 四边形中有一个内角大于90° |
18．某房地产开发公司计划建A、B两种户型的住房共80套，且A户型不超过50套．已知该公司用于本次建房的资金不超过2096万元．两种户型的建房成本和售价如下表：
（1）试求该公司对建这两种户型住房套数的选定将有哪几种方案；
（2）试问该公司采取（1）中哪种方案建房，才能使获得的利润最大？最大利润为多少万元？
| 户型 | A | B |
| 成本（万元/套） | 25 | 28 |
| 售价（万元/套） | 30 | 34 |
（2）试问该公司采取（1）中哪种方案建房，才能使获得的利润最大？最大利润为多少万元？
如图，直线a∥b，Rt△ABC的顶点B在直线a上，∠C=90°，∠β=55°，求∠α的度数．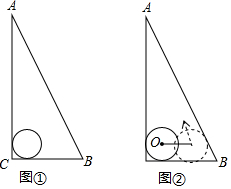
如图，△ABC是一块直角三角板，且∠C=90°，∠A=30°，现将圆心为点O的圆形纸片放置在三角板内部．
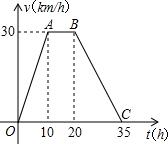据某气象站观察和预测：发生于甲地的热带风暴正向正南方向移动，其移动速度v（km/h）与时间t（h）的函数图象如图所示．