题目内容
2.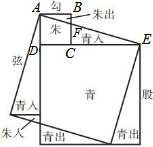 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
分析 由BF+CF求出BC的长,即为正方形ABCD的边长,由AB与CE平行,得比例求出CE的长,由DC+CE求出DE的长,在直角三角形ADE中,利用勾股定理求出AE的长即可.
解答 解:∵BF=2,CF=4,
∴BC=BF+CF=2+4=6,
∵AB∥EC,
∴$\frac{AB}{CE}$=$\frac{BF}{CF}$,即$\frac{6}{CE}$=$\frac{2}{4}$,
解得:CE=12,
在Rt△ADE中,AD=6,DE=DC+CE=6+12=18,
根据勾股定理得:AE=$\sqrt{{6}^{2}+1{8}^{2}}$=6$\sqrt{10}$,
故答案为:6$\sqrt{10}$.
点评 此题考查了勾股定理的证明,以及相似三角形的判定与性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
10.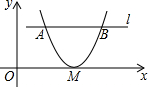 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
17.用反证法证明:在四边形中,至少有一个内角大于或等于90°,应先假设( )
| A. | 四边形中每一个内角都小于90° | |
| B. | 四边形中最多有一个内角不小于90° | |
| C. | 四边形中每一个内角都大于90° | |
| D. | 四边形中有一个内角大于90° |
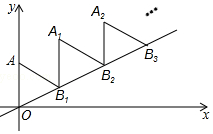 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).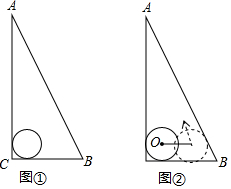 如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.