题目内容
5.二次函数y=x2-2x+m的图象与x轴的一个交点的坐标是(-1,0),则图象与x轴的另一个交点的坐标是(3,0).分析 由二次函数的解析式得出图象的对称轴,由图象的对称性即可得出答案.
解答 解:∵二次函数y=x2-2x+m的图象的对称轴为x=-$\frac{-2}{2×1}$=1,与x轴的一个交点的坐标是(-1,0),
∴由二次函数图象的对称性得:二次函数的图象与x轴的另一个交点的坐标是(3,0);
故答案为:(3,0).
点评 本题考查了抛物线与x轴的交点、二次函数的对称性、对称轴的求法;求出二次函数图象的对称轴是解决问题的关键.

练习册系列答案
相关题目
20.下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中正方形和正三角形一共有5个,第②个图形中正方形和正三角形一共有13个,第③个图形中正方形和正三角形一共有26个,…,按此规律排列下去,第⑦个图形中正方形和正三角形个数一共有( )


| A. | 60个 | B. | 77个 | C. | 78个 | D. | 168个 |
10.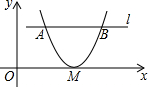 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
17.用反证法证明:在四边形中,至少有一个内角大于或等于90°,应先假设( )
| A. | 四边形中每一个内角都小于90° | |
| B. | 四边形中最多有一个内角不小于90° | |
| C. | 四边形中每一个内角都大于90° | |
| D. | 四边形中有一个内角大于90° |
 如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.
如图,在平面直角坐标系中,双曲线y=$\frac{k}{x}$与直线y=ax+b的交点A、B均在小正方形的顶点上,每个小正方形的边长均为1.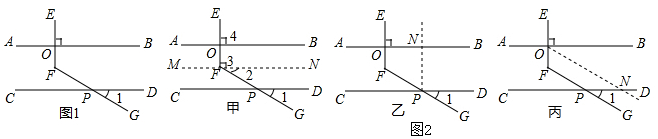
 如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.
如图,直线a∥b,Rt△ABC的顶点B在直线a上,∠C=90°,∠β=55°,求∠α的度数.