题目内容
14. 在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.
在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.
分析 由MN∥AC,得到△MN∽△BCA,于是得到△BNM和△BCA面积比为$\frac{B{N}^{2}}{B{C}^{2}}$,根据△ABD与△BMN的面积相等,且△ABD与△ABC的面积比为$\frac{BD}{BC}$,推出$\frac{B{N}^{2}}{B{C}^{2}}$=$\frac{BD}{BC}$,即可得到结论.
解答 解:∵MN∥AC,
∴△MN∽△BCA,
∴△BNM和△BCA面积比为$\frac{B{N}^{2}}{B{C}^{2}}$,
∵△ABD与△BMN的面积相等,
且△ABD与△ABC的面积比为$\frac{BD}{BC}$,
∴$\frac{B{N}^{2}}{B{C}^{2}}$=$\frac{BD}{BC}$,
∴BN2=BD•BC.
点评 本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中运用相似三角形面积比是相似比的平方的性质解题是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
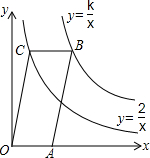 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4. 如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度.
如图,O是直线AB上的任一点,且OC⊥OD,∠1=35°,则∠2=55度. 如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是36π.
如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是36π. 如图,长方形ABCD中,AB=4cm,BC=6cm,点P,点Q同时从点B出发,点P在线段BC上运动,点Q在线段BA上运动,它们的速度均为1cm/s,当其中一点到达端点时它们同时停止运动,设运动时间为t(s).
如图,长方形ABCD中,AB=4cm,BC=6cm,点P,点Q同时从点B出发,点P在线段BC上运动,点Q在线段BA上运动,它们的速度均为1cm/s,当其中一点到达端点时它们同时停止运动,设运动时间为t(s). 如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,这时点B在边A′B′上,已知AB=5cm,BB′=2cm,则A′B的长是3cm.
如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,这时点B在边A′B′上,已知AB=5cm,BB′=2cm,则A′B的长是3cm. 关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.
关于x的不等式x-2a≤-3的解集如图所示,则a的值是1.