题目内容
4.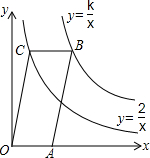 如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.
如图,已知点A在x轴上,?OABC的顶点B在反比例函数y=$\frac{k}{x}$的图象上,顶点C在反比例函数y=$\frac{2}{x}$的图象上,?OABC的面积等于4.(1)求k的值;
(2)当OA=1时,在坐标系内是否存在不同于点C的点D,使得以O、A、B、D四点为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)设OA=m,B的纵坐标是n,根据平行四边形的面积公式利用m表示出n,然后利用m表示出B和C的横坐标,根据BC=OA即可求得;
(2)首先根据(1)求得B、C的坐标,然后分成OA是一边和OA是对角线两种情况进行讨论求解.
解答 解:(1)设OA=m,B的纵坐标是n,
∵?OABC的面积等于4.
∴n=$\frac{4}{m}$,
把y=$\frac{4}{m}$代入y=$\frac{k}{x}$,得:x=$\frac{k}{\frac{4}{m}}$=$\frac{km}{4}$,
把y=$\frac{4}{m}$代入y=$\frac{2}{x}$得:x=$\frac{2}{\frac{4}{m}}$=$\frac{1}{2}$m,
根据题意得:$\frac{km}{4}$-$\frac{1}{2}$m=m,
解得:k=6;
(2)当OA=1时,A的坐标是(1,0),
B的纵坐标4,则坐标是($\frac{3}{2}$,4),C的坐标是($\frac{1}{2}$,4).
当四边形OADB是平行四边形时,则D的坐标是($\frac{5}{2}$,4);
当OA是对角线时,OA的中点是($\frac{1}{2}$,0),设D的坐标是(a,b).
则$\frac{1}{2}$(a+$\frac{3}{2}$)=$\frac{1}{2}$,$\frac{1}{2}$(4+b)=0,
解得:a=-$\frac{1}{2}$,b=-4.
则D的坐标是(-$\frac{1}{2}$,-4).
∴D的坐标是($\frac{5}{2}$,4)或(-$\frac{1}{2}$,-4).
点评 本题是反比例函数与平行四边形的综合题,根据平行四边形的性质,正确求得k的值是解决本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
13. 下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
 下列平面图形绕虚线旋转一周能形成如图立体图形的是( )
下列平面图形绕虚线旋转一周能形成如图立体图形的是( )| A. |  | B. |  | C. |  | D. |  |
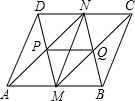 如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题:
如图,在?ABCD中,M,N分别是AB,CD的中点,AN和DM相交于点P,BN和CM相交于点Q,请思考下列问题: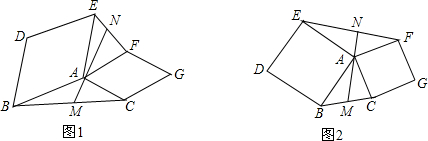
 如图,已知∠DOE=90°,OD,OE分别是∠AOC与∠BOC的平分线,A,O,B三点在同一条直线上吗?为什么?
如图,已知∠DOE=90°,OD,OE分别是∠AOC与∠BOC的平分线,A,O,B三点在同一条直线上吗?为什么? 如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论.
如图,在△ABC中,AB=AC,点D是BC的中点,BE⊥AC,垂足为E,∠ABE的平分线交AD于F.判断△DBF的形状,并证明你的结论. 在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.
在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.