Question

2．如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD=13，PC=4，则两圆组成的圆环的面积是36π．

Answer 1

分析 根据相交弦定理，求得PA的长，用勾股定理求出R²-r²的值，再由圆环的面积公式πR²-πr²，求解即可．

解答 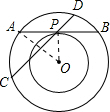解：如图，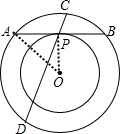

连接OP，OA，
∵AB与小圆相切于点P，
∴OP⊥AB，
∴AP=PB，
∵AP•PB=CP•DP．
∴PA²=PC•PD，CD=13，PC=4，
∴PA=6，
∵R²-r²=PA²，
∴S_圆环=π（R²-r²）=π•6²=36π．
故答案为：36π．

点评 本题考查了相交弦定理和垂径定理，以及圆环的面积，求得两个圆的半径的平方差是PA的平方是解决问题的关键．