题目内容
4.解不等式(组),并把解集表示在数轴上.(1)$\frac{3x-2}{5}$≥$\frac{2x+1}{3}$
(2)$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0}\\{3-4(x-1)<1}\end{array}\right.$.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)求出每个不等式的解集,再根据找不等式组解集的规律求出不等式组的解集即可.
解答 解:(1)$\frac{3x-2}{5}$≥$\frac{2x+1}{3}$
3(3x-2)≥5(2x+1)
9x-6≥10x+5
9x-10x≤5+6
-x≤11
x≥-11,
在数轴上表示不等式的解集为: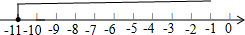 ;
;
(2)$\left\{\begin{array}{l}{1-\frac{x+1}{3}≥0①}\\{3-4(x-1)<1②}\end{array}\right.$
∵解不等式①得:x≤2,
解不等式②得:x>$\frac{3}{2}$,
∴不等式组的解集为$\frac{3}{2}$<x≤2,
在数轴上表示不等式组的解集为: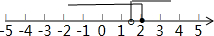 .
.
点评 本题考查了解一元一次不等式组,解一元一次不等式,在数轴上表示不等式(组)的解集的应用,能根据不等式求出不等式的解集合能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
19.若(m-1)x>m-1的解集为x<1,则m的取值范围是( )
| A. | m>1 | B. | m<1 | C. | m>0 | D. | m<0 |
9. 如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
 如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )
如图,在△ABC中,已知∠A=50°,OB、OC平分∠ABC和∠ACB,则∠BOC的度数是( )| A. | 72° | B. | 54° | C. | 46° | D. | 115° |
16.下列说法不正确的是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 有一组邻边相等、一个角是直角的四边形是正方形 |
 在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.
在△ABC中,MN∥AC,S△ABD=S△MBN,求证:BN2=BD•BC.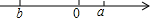 已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①.
已知实数,在数轴上的位置如图所示,则以下三个命题:①a3-ab2<0,②$\sqrt{{{(a+b)}^2}}=a+b$,③$\frac{1}{a+b}<\frac{1}{a}$,其中真命题的序号为①. 如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.
如图,把△ABC沿着AB方向平移到△A1B1C1的位置时,它们重叠部分的面积是△A1B1C1面积的一半,若AB=4,平移的距离2$\sqrt{2}$.