题目内容
5. △ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.
△ABC中,AB=AC,DE垂直平分AB(如图),∠A=25°,则∠EBC=52.5°.
分析 先利用等腰三角形的性质和三角形内角和计算出∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=77.5°,再利用线段垂直平分线的性质得AE=BE,则∠EBA=∠A=25°,然后计算∠ABC-∠EBA即可.
解答 解:∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=77.5°,
∵DE垂直平分AB,
∴AE=BE,
∴∠EBA=∠A=25°,
∴∠EBC=∠ABC-∠EBA=77.5°-25°=52.5°.
故答案为52.5°.
点评 本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等;三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
18.据国家海洋研究机构统计,中国有约1200000平方公里的海洋国土处于争议中,1200000可用科学记数法表示为( )
| A. | 1.2×105 | B. | 1.2×106 | C. | 1.2×107 | D. | 1.2×108 |
16.已知点P1(x1,y1)和点P2(x2,y2)是正比例函数y=-x+1图象上的两点,则下列判断正确的是( )
| A. | y1>y2 | B. | y1<y2 | C. | 当x1<x2时,y1>y2 | D. | 当x1<x2时,y1<y2 |
20. 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
 如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )
如图,直线y=$\frac{1}{2}$x+2交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰好落在直线y=$\frac{1}{2}$x+2上.则S△M0N=( )| A. | $\frac{12}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{16}{5}$ | D. | 4 |
15.如果单项式-xa+1y3与12ybx2是同类项,那么a、b的值分别为( )
| A. | 1,1? | B. | 2,3 | C. | 1,3? | D. | 2,1 |
 如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.
如图,△ABC内接于⊙O,∠B=30°,AC=2cm,求⊙O的半径.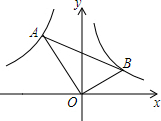 如图,Rt△AOB中,∠AOB=90°,点A在双曲线y=$\frac{k}{x}$(x<0)上,点B在双曲线y=$\frac{1}{x}$(x>0)上.
如图,Rt△AOB中,∠AOB=90°,点A在双曲线y=$\frac{k}{x}$(x<0)上,点B在双曲线y=$\frac{1}{x}$(x>0)上. 如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.
如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为3$\sqrt{5}$.