题目内容
6．
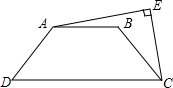如图，在等腰梯形ABCD中，AB∥CD，AB=6，CD=14，∠AEC=90°，CE=CB，则AE2=84．
分析 如图，连接AC，过点A作AF⊥CD于点F，过点B作BG⊥CD于点G，构建直角△AFC和直角△BGC，结合勾股定理求得AE2的值．
解答 解：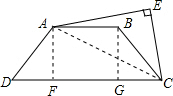
如图，连接AC，过点A作AF⊥CD于点F，过点B作BG⊥CD于点G，则AF=BG，AB=FG=6，DF=CG=4．
在直角△AFC中，AC2=AF2+FC2=AF2+102=AF2+100，
在直角△BGC中，BC2=BG2+GC2=AF2+42=AF2+16，
又∵CE=CB，∠AEC=90°，
∴AE2=AC2-EC2=AF2+100-（AF2+16）=84，即AE2=84．
故答案是：84．
点评 本题考查了等腰梯形的性质，勾股定理的应用．解题的关键是作出辅助线，构建直角三角形，利用勾股定理来求AE2的值．
练习册系列答案
相关题目
16．已知点P1（x1，y1）和点P2（x2，y2）是正比例函数y=-x+1图象上的两点，则下列判断正确的是（ ）
| A． | y1＞y2 | B． | y1＜y2 | C． | 当x1＜x2时，y1＞y2 | D． | 当x1＜x2时，y1＜y2 |
如图，若△ABC的边AB=2，AC=3，Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形，则图中三个阴影部分面积之和为3$\sqrt{5}$．
1．分式$\frac{x}{x-1}$+$\frac{1}{1-x}$可化简为（ ）
| A． | $\frac{x+1}{x-1}$ | B． | 1 | C． | -1 | D． | $\frac{x+1}{1-x}$ |
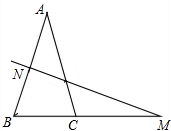如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M．
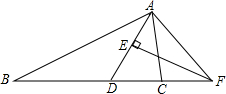如图，在△ABC中，AD平分∠BAC，EF垂直平分AD交BC的延长线于点F，判断∠CAF与∠B的大小关系，并说明理由．
15．如果单项式-xa+1y3与12ybx2是同类项，那么a、b的值分别为（ ）
| A． | 1，1? | B． | 2，3 | C． | 1，3? | D． | 2，1 |
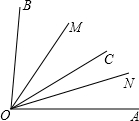如图，已知∠AOB=84°，OM、ON分别是∠BOC和∠AOC的平分线．