题目内容
16．
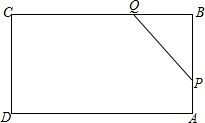如图所示，矩形ABCD中，AB=6cm，BC=12cm，点P从A出发，沿AB向点B以1m/s的速度移动，同时点Q从点B出发沿BC边向点C以2cm/s的速度（P、Q到达B、C两点后就停止运动）．若设运动第t秒时五边形CAPQCD的面积为S cm2，则S与t的函数关系式为（ ）| A． | S=t2-6t+72 | B． | S=t2+6t+72 | C． | S=t2-6t-72 | D． | S=t2+6t-72 |
分析 先利用t表示出AP=t，BQ=2t，则PB=AB-AP=6-2t，然后利用S=S矩形ABCD-S△BPQ可得到S与t的函数关系式．
解答 解：根据题意得AP=t，BQ=2t，则PB=AB-AP=6-2t，
S=S矩形ABCD-S△BPQ=12×6-$\frac{1}{2}$×2t×（6-t）=t2-6t+72（0＜0＜6）．
故选A．
点评 本题考查了根据实际问题列二次函数关系式：利用面积之间的关系建立二次函数模型，利用代数式表示有关线段是解决动点问题的关键．
练习册系列答案
相关题目
锐角△ABC中，已知∠B＞∠C，I为内心，R为外接圆半径，AD为边BC上的高线，点K在直线AD上，满足AK=2R，证明：∠KID=$\frac{∠B-∠C}{2}$．
7．
如图，∠MON=90°，点A，B分别在射线OM，ON上运动，BE平分∠NBA，BE的反向延长线与∠BAO的平分线交于点C，则∠C的度数是（ ）
如图，∠MON=90°，点A，B分别在射线OM，ON上运动，BE平分∠NBA，BE的反向延长线与∠BAO的平分线交于点C，则∠C的度数是（ ）| A． | 30° | B． | 45° | C． | 55° | D． | 60° |
电子跳蚤游戏盘如图所示的△ABC，AB=8，AC=9，BC=10，如果跳蚤开始时在BC边的点P0处，BP0=4．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1=CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2=AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3=BP2；跳蚤按上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2015与A间的距离为（ ）
如图，∠AOB=∠COD=90°，∠AOD=132°，则∠BOC=48°．
8．
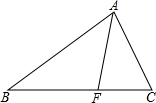如图△ABC中，AF平分∠BAC，F是BC上的一点，且BF=2CF，AC=1，则AB=（ ）
如图△ABC中，AF平分∠BAC，F是BC上的一点，且BF=2CF，AC=1，则AB=（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 6 |
如图，△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为40°．