题目内容
6. 锐角△ABC中,已知∠B>∠C,I为内心,R为外接圆半径,AD为边BC上的高线,点K在直线AD上,满足AK=2R,证明:∠KID=$\frac{∠B-∠C}{2}$.
锐角△ABC中,已知∠B>∠C,I为内心,R为外接圆半径,AD为边BC上的高线,点K在直线AD上,满足AK=2R,证明:∠KID=$\frac{∠B-∠C}{2}$.
分析 连接AI并延长交BC于E,交⊙O于T.连接CI、CT、,连接AO并延长交⊙O于M,连接MC、MT、KT.首先证明∠DAI=$\frac{1}{2}$(∠B-∠C),想办法证明△KID∽△KAI,推出∴∠KID=∠DAT=$\frac{1}{2}$(∠B-∠C),即可解决问题.
解答 证明:连接AI并延长交BC于E,交⊙O于T.连接CI、CT、,连接AO并延长交⊙O于M,连接MC、MT、KT.
∵I是内心,AD⊥BC,
∴∠CAI=∠BAI,∠ADB=∠ADC=90°,
∴∠DAT=∠CAD-∠CAI=90°-∠ACB-$\frac{1}{2}$[180°-(∠B+∠ACB)]=$\frac{1}{2}$(∠B-∠C),
∵∠CIT=∠CAJ+∠ACI,∠ICT=∠ICB+∠TCB,∠CAI=∠BAI=∠BCT,∠ACI=∠ICB,
∴∠ICT=∠CIT,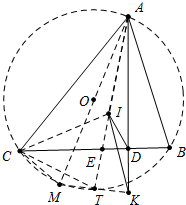
∴CT=IT,
∵∠CTI=∠CTA,∠ECT=∠CAT,
∴△TCE∽△TAC,
∴TC2=TE•TA,即TI2=TE•TA,
∵∠CAM=∠DAB,
∴∠TAM=∠DAT,∵AM=AK,AT=AT,
∴△AMT≌△AKT,
∴∠ATK=∠ATM=90°,TK=TM,
∵∠ETk+∠EDK=180°,
∴E、D、K、T四点共圆,
∴AD•AK=AE•AT,
∴AK2-AD•AK=AK2-AE•AT,即KD•AK=4R2-AE•AT,
∵IK2=IT2+TK2=TE•TA+MT2=TE•TA+AM2-AI2=AM2-(AT2-TE•TA)=4R2-AT•AE,
∴IK2=KD•AK,∵∠IKD=∠AKI,
∴△KID∽△KAI,
∴∠KID=∠DAT=$\frac{1}{2}$(∠B-∠C).
点评 本题考查内心、外心、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题,题目比较难,条件的辅助线比较多,属于竞赛类题目.

 如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )
如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是( )| A. | 60° | B. | 80° | C. | 100° | D. | 120° |
| A. | x1=x2=2 | B. | x1=x2=$\frac{1}{2}$ | C. | x1=x2=-2 | D. | x1=x2=-$\frac{1}{2}$ |
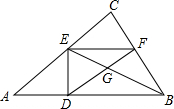 如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )
如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,AB上有一动点D以每秒4个单位的速度从点A向点B运动,当点D运动到点B时停止运动.过点D作DE⊥AB,垂足为点D,过点E作EF∥AB交BC于点F,连接BE交DF于点G,设点D运动的时间为t,当S△BDG=4S△EFG时,t的值为( )| A. | t=$\frac{14}{17}$ | B. | t=$\frac{12}{10}$ | C. | t=$\frac{10}{17}$ | D. | t=$\frac{8}{17}$ |
| A. | 35 | B. | 40 | C. | 45 | D. | 50 |
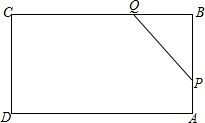 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )| A. | S=t2-6t+72 | B. | S=t2+6t+72 | C. | S=t2-6t-72 | D. | S=t2+6t-72 |
 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.