题目内容
1.定义运算*为:a*b=$\left\{\begin{array}{l}{ab(b>0)}\\{-ab(b≤0)}\end{array}\right.$如:1*(-2)=-1×(-2)=2,则函数y=2*x的图象大致是( )| A. | 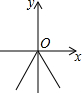 | B. |  | C. |  | D. |  |
分析 根据定义运算“※”为:a*b=$\left\{\begin{array}{l}{ab(b>0)}\\{-ab(b≤0)}\end{array}\right.$,可得y=2※x的函数解析式,根据函数解析式,可得函数图象.
解答 解:y=2※x=$\left\{\begin{array}{l}{2x(x>0)}\\{-2x(x≤0)}\end{array}\right.$,
x>0时,图象是y=2x的正比例函数中y轴右侧的部分;x≤0时,图象是y=-2x的正比例函数中y左侧的部分,
故选:C.
点评 本题考查了正比例函数的图象,利用定义运算“※”为:a*b=$\left\{\begin{array}{l}{ab(b>0)}\\{-ab(b≤0)}\end{array}\right.$,得出分段函数是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
| A. | 35 | B. | 40 | C. | 45 | D. | 50 |
12.下列各式中一定成立的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{7}$+$\sqrt{3}$=$\sqrt{10}$ | C. | $\sqrt{{x}^{2}}$=|x| | D. | ($\sqrt{-x}$)2=x |
16.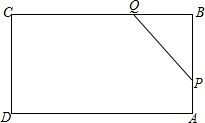 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )| A. | S=t2-6t+72 | B. | S=t2+6t+72 | C. | S=t2-6t-72 | D. | S=t2+6t-72 |
13. 如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
 如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )| A. | k<-3 | B. | k>-3 | C. | k<3 | D. | k>3 |
 如图,直线l经过点A(1,0),且与双曲线$y=\frac{m}{x}({x>0})$交于点B(2,1),
如图,直线l经过点A(1,0),且与双曲线$y=\frac{m}{x}({x>0})$交于点B(2,1), 如图,∠A=∠BDC=90°,∠ACB=∠DBC,AB=5,BD=12,BC=13,则点D到边BC的距离为$\frac{60}{13}$.
如图,∠A=∠BDC=90°,∠ACB=∠DBC,AB=5,BD=12,BC=13,则点D到边BC的距离为$\frac{60}{13}$.