题目内容
11．
如图，∠AOB=∠COD=90°，∠AOD=132°，则∠BOC=48°．
分析 根据角的和差，可得∠AOC的度数，根据余角的性质，可得答案．
解答 解：由角的和差，得
∠AOC=∠AOD-∠COD=132°-90°=42°．
由余角的性质，得
∠COB=90°-∠AOC=90°-42°=48°，
故答案为：48．
点评 本题考查了余角和补角，利用了余角的性质，角的和差，结合图形运算是解答此题的关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
1．
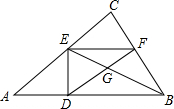如图所示，在Rt△ABC中，∠C=90°，AC=4，BC=3，AB上有一动点D以每秒4个单位的速度从点A向点B运动，当点D运动到点B时停止运动．过点D作DE⊥AB，垂足为点D，过点E作EF∥AB交BC于点F，连接BE交DF于点G，设点D运动的时间为t，当S△BDG=4S△EFG时，t的值为（ ）
如图所示，在Rt△ABC中，∠C=90°，AC=4，BC=3，AB上有一动点D以每秒4个单位的速度从点A向点B运动，当点D运动到点B时停止运动．过点D作DE⊥AB，垂足为点D，过点E作EF∥AB交BC于点F，连接BE交DF于点G，设点D运动的时间为t，当S△BDG=4S△EFG时，t的值为（ ）| A． | t=$\frac{14}{17}$ | B． | t=$\frac{12}{10}$ | C． | t=$\frac{10}{17}$ | D． | t=$\frac{8}{17}$ |
19．
如图，已知平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，下面结论：
①DB=$\sqrt{2}$BE；②∠BAD=∠BHE；③AB=BH；④$\frac{A{C}^{2}+B{D}^{2}}{B{C}^{2}+D{C}^{2}}$=2
其中正确的有（ ）
如图，已知平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，下面结论：①DB=$\sqrt{2}$BE；②∠BAD=∠BHE；③AB=BH；④$\frac{A{C}^{2}+B{D}^{2}}{B{C}^{2}+D{C}^{2}}$=2
其中正确的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
6．已知a≥0，b≥0，且a+b=2，则（ ）
| A． | ab≤$\frac{1}{2}$ | B． | ab≥$\frac{1}{2}$ | C． | a2+b2≥2 | D． | a2+b2≤3 |
16．
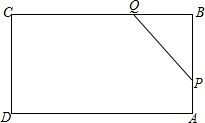如图所示，矩形ABCD中，AB=6cm，BC=12cm，点P从A出发，沿AB向点B以1m/s的速度移动，同时点Q从点B出发沿BC边向点C以2cm/s的速度（P、Q到达B、C两点后就停止运动）．若设运动第t秒时五边形CAPQCD的面积为S cm2，则S与t的函数关系式为（ ）
如图所示，矩形ABCD中，AB=6cm，BC=12cm，点P从A出发，沿AB向点B以1m/s的速度移动，同时点Q从点B出发沿BC边向点C以2cm/s的速度（P、Q到达B、C两点后就停止运动）．若设运动第t秒时五边形CAPQCD的面积为S cm2，则S与t的函数关系式为（ ）| A． | S=t2-6t+72 | B． | S=t2+6t+72 | C． | S=t2-6t-72 | D． | S=t2+6t-72 |
如图，?ABCD中，BC=2AB，E为AD中点，过点C作CF⊥AB于点F，垂足F落在线段AB上，连结FE并延长与CD的延长线交于点G，则下列结论：①CE平分∠BCG；②CE=EF；③∠DEF=3∠AFE；④当AF=BF时，S△BCF=S△CEF，正确的有（ ）
如图，已知⊙O经过点A（2，0）、C（0，2），直线y=kx与⊙O分别交于点B、D，则四边形ABCD面积的最大值为4$\sqrt{2}$．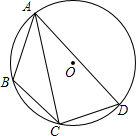
在⊙O的内接四边形ABCD中，AB=6，AD=10，∠BAD=60°，点C为弧BD的中点，则AC的长是$\frac{16}{3}$$\sqrt{3}$．