题目内容
8.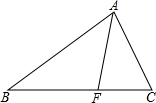 如图△ABC中,AF平分∠BAC,F是BC上的一点,且BF=2CF,AC=1,则AB=( )
如图△ABC中,AF平分∠BAC,F是BC上的一点,且BF=2CF,AC=1,则AB=( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 根据FE∥AC交AB于E,ED∥BC交AC于D可得到四边形EFCD为平行四边形,从而得到EF=DC,再根据AF平分△ABC的∠BAC交BC于F,得到AE=EF,利用平行线分线段成比例定理即可求得.
解答 解:∵AF平分△ABC的∠BAC交BC于F,
∴∠BAF=∠CAF,
∵FE∥AC交AB于E,
∴∠CAF=∠AFE,
∴∠EAF=∠EFA,
∴AE=FE,
∵FE∥AC交AB于E,ED∥BC交AC于D
∴四边形EFCD为平行四边形,
∴AE=EF=DC,
∵FE∥AC交AB于E,BF=2CF,AC=1,
∴$\frac{BE}{AE}=\frac{BF}{CF}=\frac{2}{1},\frac{AE}{AB}=\frac{AD}{AC}$,
解得AE=$\frac{1}{3}$,
∴AB=1,
故选A.
点评 本题考查了平行四边形的判定及性质和平行线分线段成比例定理的知识,解题的关键是得到AE=EF=DC.

练习册系列答案
相关题目
19. 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
①DB=$\sqrt{2}$BE;②∠BAD=∠BHE;③AB=BH;④$\frac{A{C}^{2}+B{D}^{2}}{B{C}^{2}+D{C}^{2}}$=2
其中正确的有( )
 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:①DB=$\sqrt{2}$BE;②∠BAD=∠BHE;③AB=BH;④$\frac{A{C}^{2}+B{D}^{2}}{B{C}^{2}+D{C}^{2}}$=2
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.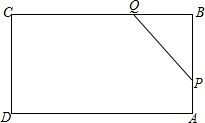 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
 如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )
如图所示,矩形ABCD中,AB=6cm,BC=12cm,点P从A出发,沿AB向点B以1m/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度(P、Q到达B、C两点后就停止运动).若设运动第t秒时五边形CAPQCD的面积为S cm2,则S与t的函数关系式为( )| A. | S=t2-6t+72 | B. | S=t2+6t+72 | C. | S=t2-6t-72 | D. | S=t2+6t-72 |
3. 如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )
如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )
 如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )
如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
13. 如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
 如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是( )| A. | k<-3 | B. | k>-3 | C. | k<3 | D. | k>3 |
 如图,已知⊙O经过点A(2,0)、C(0,2),直线y=kx与⊙O分别交于点B、D,则四边形ABCD面积的最大值为4$\sqrt{2}$.
如图,已知⊙O经过点A(2,0)、C(0,2),直线y=kx与⊙O分别交于点B、D,则四边形ABCD面积的最大值为4$\sqrt{2}$. 如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1,S2,若S1=2,S2=3,AB2=5,则△ABC的形状是直角三角形.
如图,以△ABC的两边BC、AC分别向外作正方形,它们的面积分别是S1,S2,若S1=2,S2=3,AB2=5,则△ABC的形状是直角三角形.