题目内容
4.画出任一矩形ABCD的最小覆盖圆,画一个矩形ABCD中,AB=2cm,BC=4cm,若两个等圆完全覆盖这个矩形,请求出这两个等圆的最小半径.分析 连任意矩形ABCD的对角线,交点即为圆心、对角线的一半为半径即为所求作圆;分别连接AC、BD交于点P,过点P作EF⊥AD于点E,交BC于点F,可得四边形ABFE是正方形,连接BE、AF交于点O1,连接DF、CE交于点O2,分别以O1、O2为圆心,O1A、O2D为半径画圆即为所求作圆,继而可得最小圆的半径.
解答 解:任意矩形ABCD的最下覆盖圆如图1所示,⊙O即为所求;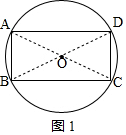
如图2,AB=2cm,BC=4cm,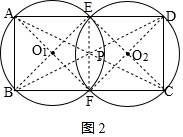
分别连接AC、BD,交于点P,
∴AP=PC,
过点P作EF⊥AD于点E,交BC于点F,
∴PE∥CD,
则AE=DE=AB=2cm,
∴四边形ABFE是正方形,
连接BE、AF交于点O1,连接DF、CE交于点O2,
分别以O1、O2为圆心,O1A、O2D为半径画圆,
则O1A=O1B=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$cm,
即这两个等圆的最小半径为$\sqrt{2}$cm.
点评 本题主要考查矩形的性质和圆的定义,熟练掌握矩形的对角线相等并且平分和到顶点的距离等于定长的所有点的集合是圆是解题的关键.

练习册系列答案
相关题目
13.某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表所示:
(1)若商场购进的甲型节能灯500只,则购买甲、乙两种节能灯共需多少元?
(2)若商场购进甲型节能灯x只,则购买甲、乙两种节能灯共需-20x+54000元;(用含x的代数式表示)
(3)如何进货,商场销售完节能灯时恰好获利30%,此时利润为多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)若商场购进甲型节能灯x只,则购买甲、乙两种节能灯共需-20x+54000元;(用含x的代数式表示)
(3)如何进货,商场销售完节能灯时恰好获利30%,此时利润为多少元?
16.若“?”是某种新规定的运算符号,设a?b=3a+2b,则[(x+y)?(x-y)]?3x化简为( )
| A. | 0 | B. | 21x+3y | C. | 5x | D. | 9x+6y |
 如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系.
如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系. 如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.
如图所示,已知点E是四边形ABCD内的一点,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,试说明AD与BC的位置关系.