题目内容
9.(1)$\frac{9}{4}$x2-y2=($\frac{3}{2}$x+y)($\frac{3}{2}$x-y). (2)$\frac{4}{25}$x2-$\frac{9}{16}$y2=($\frac{2}{5}$x+$\frac{3}{4}$y)($\frac{2}{5}$x-$\frac{3}{4}$y).(3)a4-1=(a2+1)(a+1)(a-1). (4)a2-(c+b)2=(a+c+b)(a-c-b).
(5)(a-b)2-(b+a)2=-4ab.(6)a3-a(b-c)2=a(a+b-c)(a-b+c).
分析 (1)原式利用平方差公式分解即可;
(2)原式利用平方差公式分解即可;
(3)原式利用平方差公式分解即可;
(4)原式利用平方差公式分解即可;
(5)原式利用平方差公式计算即可;
(6)原式提取公因式,再利用平方差公式分解即可.
解答 解:(1)$\frac{9}{4}$x2-y2=($\frac{3}{2}$x+y)($\frac{3}{2}$x-y);
(2)$\frac{4}{25}$x2-$\frac{9}{16}$y2=($\frac{2}{5}$x+$\frac{3}{4}$y)($\frac{2}{5}$x-$\frac{3}{4}$y);
(3)a4-1=(a2-1)(a2+1)=(a2+1)(a+1)(a-1);
(4)a2-(c+b)2=(a+c+b)(a-c-b);
(5)(a-b)2-(b+a)2=-4ab;
(6)a3-a(b-c)2=a(a+b-c)(a-b+c),
故答案为:(1)($\frac{3}{2}$x+y)($\frac{3}{2}$x-y);(2)($\frac{2}{5}$x+$\frac{3}{4}$y)($\frac{2}{5}$x-$\frac{3}{4}$y);(3)(a2+1)(a+1)(a-1);(4)(a+c+b)(a-c-b);(5)-4ab;(6)a(a+b-c)(a-b+c)
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
17.某公交公司有A、B两种客车,它们的载客数量和租金如表;
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送八年级师生到基地校参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题;
(1)用含x的式子填写表格
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
| A | B | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 280 |
(1)用含x的式子填写表格
| 车辆数(辆) | 载客量 | 租金(元) | |
| A | x | 45x | 400x |
| B | 5-x | 30(5-x) | 280(5-x) |
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
14. 如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=( )
如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=( )
 如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=( )
如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=( )| A. | 78° | B. | 80° | C. | 50° | D. | 60° |
18.按键 能计算出下列哪个式子的值( )
能计算出下列哪个式子的值( )
 能计算出下列哪个式子的值( )
能计算出下列哪个式子的值( )| A. | (-4)5+1 | B. | -(45+2) | C. | -45+2 | D. | 45-2 |
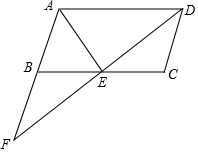 如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.
如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.