题目内容
12.定义运算“△”:对于任意实数a,b且a≥b时,都有a△b=a2-ab+b2,如5△4=52-5×4+42=21,若(x-3)△4=21,则实数x的值为8.分析 根据新定义得出关于x的方程(x-3)2-4(x-3)+16=21,整理得(x-3)2-4(x-3)-5=0,将x-3看做整体因式分解法求解得出x的值,再结合x-3≥4取舍即可得.
解答 解:根据题意得(x-3)2-4(x-3)+16=21,
即(x-3)2-4(x-3)-5=0,
∴(x-3+1)(x-3-5)=0,即(x-2)(x-8)=0,
解得:x=2或x=8,
又∵x-3≥4,即x≥7,
∴x=8,
故答案为:8.
点评 本题主要考查新定义下一元二次方程的解法及解不等式的能力,根据新定义列出关于x的方程并熟练掌握解一元二次方程的能力是解题的关键.

练习册系列答案
相关题目
17.某公交公司有A、B两种客车,它们的载客数量和租金如表;
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送八年级师生到基地校参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题;
(1)用含x的式子填写表格
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
| A | B | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 280 |
(1)用含x的式子填写表格
| 车辆数(辆) | 载客量 | 租金(元) | |
| A | x | 45x | 400x |
| B | 5-x | 30(5-x) | 280(5-x) |
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.

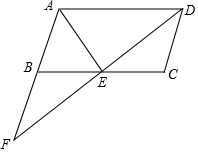 如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.
如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.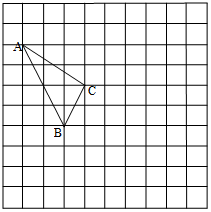 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,3)、(-1,1).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,3)、(-1,1).