题目内容
14. 如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系.
如图,AB∥CD,试找出∠B、∠C、∠BEC三者之间的数量关系.
分析 过点E作EF∥AB,由平行线的性质可知,AB∥CD∥EF,故可得∠B+∠1=180°,∠2=∠C,由此即可得出结论.
解答  解:过点E作EF∥AB,
解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠B+∠1=180°①,∠2=∠C②,
∴①+②得,∠B+∠1+∠2=180°+∠C,
即∠B+∠BEC-∠C=180°.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5. 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校60名学生体育测试成绩成绩统计表
(说明:40-55分为不合格,55-70分为合格,70-85分为良好,85-100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的a=18;b=0.5;c=3;d=0.05.
(2)请根据频数分布表,画出相应的频数分布直方图.
 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩成绩统计表
| 成绩 | 划记 | 频数 | 频率 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 |   | c | d |
| 合计 |
请根据以上信息,解答下列问题:
(1)表中的a=18;b=0.5;c=3;d=0.05.
(2)请根据频数分布表,画出相应的频数分布直方图.
5.关于$\sqrt{5}$的叙述,正确的是( )
| A. | $\sqrt{5}$是有理数 | B. | 5的平方根是$\sqrt{5}$ | ||
| C. | 2<$\sqrt{5}$<3 | D. | 在数轴上不能找到表示$\sqrt{5}$的点 |
 如图,∠AOC与∠BOC互为邻补角,OE平分∠AOC,OF平分∠BOC,试说明:OE⊥OF.
如图,∠AOC与∠BOC互为邻补角,OE平分∠AOC,OF平分∠BOC,试说明:OE⊥OF.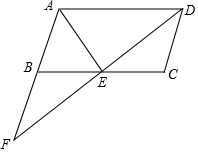 如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.
如图,在?ABCD中,E是BC边的中点,DE与AB的延长线交于点F.