题目内容
1.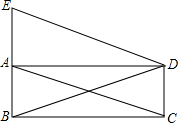 如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E.
如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E.(1)判断△DBE的形状等腰三角形;
(2)证明你的结论.
分析 (1)可以证明DE=DB,结论是△DBE是等腰三角形.
(2)先证明四边形AEDC是平行四边形,得到AC=ED,根据矩形的性质得到AC=BD,由此即可证明.
解答 (1)解:△DBE是等腰三角形.
故答案为等腰三角形.
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD,AC=BD,
∵DE∥AC,AE∥CD,
∴四边形AEDC是平行四边形,
∴AC=DE,
∴DE=DB,
∴△DBE是等腰三角形.
点评 本题考查了矩形的性质、平行四边形的判定和性质、等腰三角形的判定等知识,解题的关键是灵活应用这些知识,属于中考常考题型.

练习册系列答案
相关题目
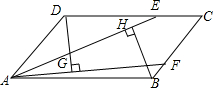 如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.
如图,在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,DG⊥AE,BH⊥AF,点G,H为垂足,猜想DG与BH的大小关系,并证明你的猜想.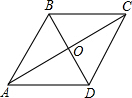 如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm,求对角线BD的长和菱形ABCD的面积.
如图,菱形ABCD的周长为20cm,对角线AC、BD相交于点O,AC=8cm,求对角线BD的长和菱形ABCD的面积.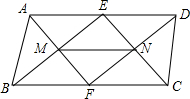 如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
如图所示,已知在?ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.