题目内容
12．
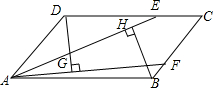如图，在平行四边形ABCD中，点E，F分别在BC，CD上，且AE=AF，DG⊥AE，BH⊥AF，点G，H为垂足，猜想DG与BH的大小关系，并证明你的猜想．
分析 首先连接DF，BE，易得S△ADF=S△ABE=$\frac{1}{2}$S?ABCD，又由AE=AF，DG⊥AF，BH⊥AE，利用面积法，即可证得结论．
解答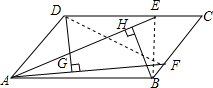 
证明：连接DF，BE，
∵点E，F分别在?ABCD的边DC，CB上，
∴S△ADF=$\frac{1}{2}$S?ABCD，S△ABE=$\frac{1}{2}$S?ABCD，
∴S△ADF=S△ABE，
∵DG⊥AF，BH⊥AE，
∴$\frac{1}{2}$AF•DG=$\frac{1}{2}$AE•BH，
∵AE=AF，
∴DG=BH．
点评 此题考查了平行四边形的性质．注意利用S△ADF=S△ABE求解是解此题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
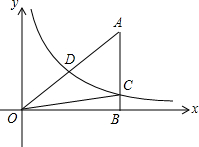如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象交Rt△OAB的斜边OA于点D，交直角边AB于点C，点B在x轴上，若△OAC的面积为5，OA：OD=2：1，则k的值为8．
如图，在?ABCD中，AB=2BC，E为AB的中点，DF⊥BC，垂足为F．请你说明：∠AED=∠EFB．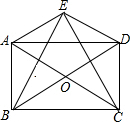
如图，点E为?ABCD外一点，AE⊥EC，BE⊥ED，对角线AC、BD相交于点O．
如图．E是?ABCD内任一点，若S?ABCD=6，则S△ABE+S△CDE=3．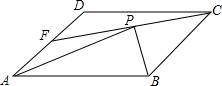
在平行四边形ABCD中，F是AD的中点，BP⊥CF交于点P，若AP=2$\sqrt{3}$，求AB的长．
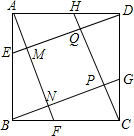已知，如图，E，F，G，H分别是正方形ABCD各边的中点，AF，BC，CH，DE分别相交于点M，N，P，Q．求证：四边形MNPQ是正方形．
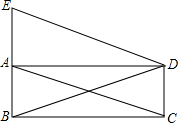如图，矩形ABCD中，AC，BD是对角线，过顶点D作AC的平行线与BA的延长线相交于点E．
如图所示，在?ABCD中，M，N是对角线BD上的两点，BN=DM，请判断AM与CN有怎样的数量关系，并说明理由，它们的位置关系如何呢？