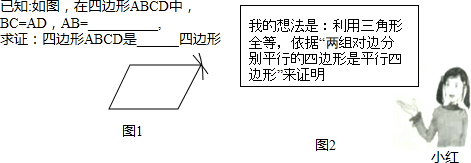
题目内容
11.菱形面积为8$\sqrt{3}$cm2,两对角线之比为1:$\sqrt{3}$,则边长为4,相邻两内角度数是60°,120°.分析 设菱形的两条对角线的长分别是x,$\sqrt{3}$x,根据菱形的面积是两条对角线乘积的一半,可建立方程,解方程求出x的值即可求出其边长和菱形内角的度数.
解答 解:
∵菱形两对角线之比为1:$\sqrt{3}$,
∴设菱形的两条对角线的长分别是x,$\sqrt{3}$x,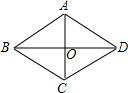
∵菱形面积为8$\sqrt{3}$cm2,
∴$\frac{1}{2}$x•$\sqrt{3}$x=8$\sqrt{3}$,
∴x=4,
∵菱形两对角线之比为1:$\sqrt{3}$,
∴tan∠OBC=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠OBC=30°,
∴∠ABC=60°,
∴∠BAD=120°,
故答案为:4,60°,120°.
点评 此题主要考查菱形的性质,难度一般,注意掌握菱形面积等于两条对角线的积的一半是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y=$\frac{k}{x}(k>0)$的图象上,则y1,y2,y3的大小关系为( )
| A. | y1<y3<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
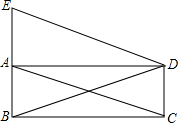 如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E.
如图,矩形ABCD中,AC,BD是对角线,过顶点D作AC的平行线与BA的延长线相交于点E. 如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?
如图所示,在?ABCD中,M,N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由,它们的位置关系如何呢?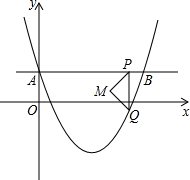 如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-2)2-2与y轴交于点A(0,1),直线AB∥x轴交抛物线于点B,点P是直线AB上一点(不与A、B重合),PQ∥y轴交抛物线于点Q,以PQ为斜边向左作等腰直角三角形PQM,设点P的横坐标为m.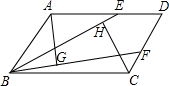 已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.
已知:如图,在平行四边形ABCD中,E、F分别为边AD、CD上一点,且BE=BF,AG⊥BF于F,CH⊥BE于H,求证:AG=CH.