题目内容
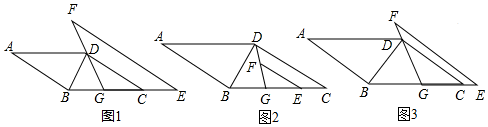
13.平行四边形ABCD中,∠ABD=90°,G点为BC边上一点,连结DG,E点在BC边所在直线上,过E点作EF∥CD交GD于F点.(1)如图1,若G为BC边中点,EF交GD延长线于F点,tanA=$\frac{1}{2}$,CE=CG,DG=$\sqrt{5}$,求EF;
(2)如图2,若E点在BC边上,G为BE中点,且GD平分∠BDC,求证:$\sqrt{2}$DB=2FG+DF;
(3)如图3,若E点在BC延长线上,G为BE中点,且∠GDC=30°,问(2)中结论还成立吗?若不成立,那么线段DB、FG、DF满足怎样的数量关系,请直接写出结论.
分析 (1)先根据直角三角形斜边上中线的性质,求得BC的长,再根据勾股定理,求得CD的长,最后根据三角形中位线定理,求得EF的长即可;
(2)先延长DG交AB的延长线于H点,根据GD平分∠BDC,得到△BDH是等腰直角三角形,得出DH=$\sqrt{2}$DB,然后判定△BGH≌△EGF(AAS),得到GH=FG,最后根据DH=FH+DF,即可得到$\sqrt{2}$DB=2FG+DF;
(3)先延长DG交AB的延长线于H点,根据∠GDC=∠H=30°,得出DH=2DB,然后判定△BGH≌△EGF(AAS),得到GH=FG,最根据DH=FH-DF,即可得到2DB=2FG-DF.
解答  解:(1)如图1,在平行四边形ABCD中,AB∥CD,
解:(1)如图1,在平行四边形ABCD中,AB∥CD,
∴∠BDC=∠ABD=90°,
∵在Rt△BDC中,G为BC的中点,DG=$\sqrt{5}$,
∴BC=2DG=2$\sqrt{5}$,
又∵tanA=tan∠BCD=$\frac{1}{2}$,
∴CD=2BD,
故可设BD=x,CD=2x,则
Rt△BCD中,x2+(2x)2=(2$\sqrt{5}$)2,
解得x=2,
∴CD=4,
又∵CE=CG,CD∥EF,
∴D为GF的中点,
∴EF=2CD=8;
(2)如图2,延长DG交AB的延长线于H点,则∠DBH=90°,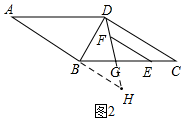
∵AB∥CD,
∴∠BDC=∠ABD=90°,
又∵GD平分∠BDC,
∴∠BDH=∠CDH=45°,
∴△BDH是等腰直角三角形,
∴DH=$\sqrt{2}$DB,
又∵EF∥CD,
∴EF∥AB,
∴∠F=∠H,∠E=∠HBG,
又∵G为BE的中点,
∴BG=EG,
∴△BGH≌△EGF(AAS),
∴GH=FG,
∵DH=FH+DF,
∴$\sqrt{2}$DB=2FG+DF;
(3)若E点在BC延长线上,G为BE中点,且∠GDC=30°,则(2)中的结论不成立,正确结论为:2DB=2FG-FD.
证明:如图3,延长DG交AB的延长线于H点,则∠DBH=90°,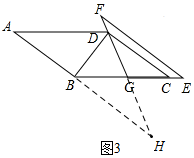
∵AB∥CD,
∴∠GDC=∠H=30°,
∴DH=2DB,
又∵EF∥CD,
∴EF∥AB,
∴∠F=∠H,∠E=∠HBG,
又∵G为BE的中点,
∴BG=EG,
∴△BGH≌△EGF(AAS),
∴GH=FG,
∵DH=FH-DF,
∴2DB=2FG-DF.
点评 本题主要考查了全等三角形的判定与性质、直角三角形斜边上的中线的性质、等腰直角三角形的性质、含30°角的直角三角形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行求解.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;在直角三角形中,斜边上的中线等于斜边的一半.

 已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题: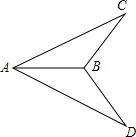 如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.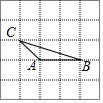 如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )
如图,由25个同样大小的小正方形组成的正方形网格中,△ABC是格点三角形(每个顶点都是格点),在这个正方形网格中画另一个格点三角形,使得它与△ABC全等且仅有一条公共边,则符合要求的三角形共能画( )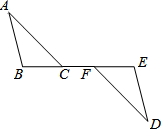 如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.
如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.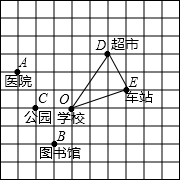 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题: