题目内容
3.将抛物线y=$\frac{1}{3}$x2-$\frac{4}{3}$x+1向左平移2个单位,再向上平移$\frac{1}{3}$个单位,就能得到函数y=$\frac{1}{3}$x2的图象.分析 直接利用配方法得出抛物线的顶点式,进而利用二次函数平移的性质得出答案.
解答 解:y=$\frac{1}{3}$x2-$\frac{4}{3}$x+1
=$\frac{1}{3}$(x2-4x)+1
=$\frac{1}{3}$(x-2)2-$\frac{1}{3}$,
故将抛物线y=$\frac{1}{3}$x2-$\frac{4}{3}$x+1向左平移2个单位,再向上平移$\frac{1}{3}$个单位,就能得到函数y=$\frac{1}{3}$x2的图象.
故答案为:左,2,上,$\frac{1}{3}$.
点评 此题主要考查了二次函数图象与几何变换,正确掌握平移规律是解题关键.

练习册系列答案
相关题目
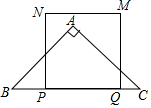 如图,在△ABC中,∠BAC=90°,AB=AC,BC=12cm,动点P从点B出发,以2cm/s的速度沿BC向点C运动,动点Q从点C出发,以1cm/s的速度沿CB向点B运动,当点P与Q相遇时,则同时停止运动,点P出发后,以线段PQ为边向上作正方形PQMN,设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s)
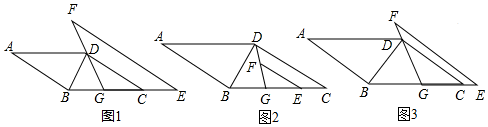
如图,在△ABC中,∠BAC=90°,AB=AC,BC=12cm,动点P从点B出发,以2cm/s的速度沿BC向点C运动,动点Q从点C出发,以1cm/s的速度沿CB向点B运动,当点P与Q相遇时,则同时停止运动,点P出发后,以线段PQ为边向上作正方形PQMN,设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s) 如图,点E在直线DF上,点B在直线AC上,已知∠1=∠2,∠C=∠D.请问∠A=∠F吗?为什么?
如图,点E在直线DF上,点B在直线AC上,已知∠1=∠2,∠C=∠D.请问∠A=∠F吗?为什么?