题目内容
6. 如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )
如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
分析 根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
解答 解:菱形对角线互相垂直平分,
∴BO=OD=3,AO=OC=4,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5,
∴菱形的周长=4AB=20.
故选A.
点评 本题考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.

练习册系列答案
相关题目
17.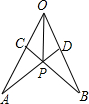 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
1.下面是三角形三边的比,其中是直角三角形三边的比的是( )
| A. | 2:1:2 | B. | 2:3:4 | C. | 1:1:$\sqrt{2}$ | D. | 4:5:6 |
15.若$\frac{|x|-2}{{x}^{2}-x-2}$=0,则x等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
 已知,∠α
已知,∠α