题目内容
11.计算:2$\sqrt{\frac{a}{2}}$-3$\sqrt{\frac{a}{8}}$+$\sqrt{32a}$.分析 先把各二次根式化为最简二次根式,再合并同类项即可.
解答 解:原式=$\sqrt{2a}$-$\frac{3}{4}$$\sqrt{2a}$+4$\sqrt{2a}$
=(1-$\frac{3}{4}$+4)$\sqrt{2a}$
=$\frac{17}{4}$$\sqrt{2a}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
6. 如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )
如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )
 如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )
如图所示,在菱形ABCD中,AC=8,BD=6,则菱形的周长为( )| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
3.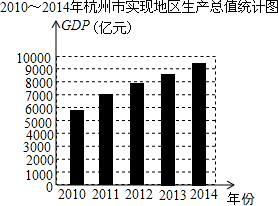 根据2010~2014年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( )
根据2010~2014年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( )
 根据2010~2014年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( )
根据2010~2014年杭州市实现地区生产总值(简称GDP,单位:亿元)统计图所提供的信息,下列判断正确的是( )| A. | 2012~2014年杭州市每年GDP增长率相同 | |
| B. | 2014年杭州市的GDP比2010年翻一番 | |
| C. | 2010年杭州市的GDP未达到5400亿元 | |
| D. | 2010~2014年杭州市的GDP逐年增长 |
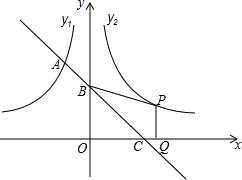 如图,一次函数y=-x+b的图象与反比例函数y1=$\frac{{k}_{1}}{x}$(x<0)的图象相交于A(a,3)点,与y轴,x轴分别相交于B,C两点,且点C的坐标为(2,0).
如图,一次函数y=-x+b的图象与反比例函数y1=$\frac{{k}_{1}}{x}$(x<0)的图象相交于A(a,3)点,与y轴,x轴分别相交于B,C两点,且点C的坐标为(2,0).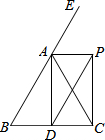 如图,△ABC中,AB=AC,D是BC边的中点,E是BA延长线上一点,AP平分∠EAC,DP∥AB交AP于点P,求证:四边形ADCP是矩形.
如图,△ABC中,AB=AC,D是BC边的中点,E是BA延长线上一点,AP平分∠EAC,DP∥AB交AP于点P,求证:四边形ADCP是矩形.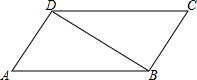 如图,平行四边形ABCD的边长AD=3cm,AB=8cm,∠A=60°,现求对角线BD的长度.
如图,平行四边形ABCD的边长AD=3cm,AB=8cm,∠A=60°,现求对角线BD的长度. 如图,
如图,