题目内容
14. 如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.(1)如果$\frac{AD}{AB}$=$\frac{2}{3}$,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
分析 (1)由DE与BC平行,得到两对同位角相等,进而得到三角形ADE与三角形ABC相似,由相似得比例求出BC的长即可;
(2)由两直线平行得到一对同位角相等,再由已知角相等等量代换得到∠FAE=∠ADF,根据公共角相等,得到三角形AEF与三角形ADF相似,由相似得比例求出DF的长即可.
解答 解:(1)∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{2}{3}$,
∵DE=6,
∴BC=9;
(2)∵DE∥BC,
∴∠B=∠ADE,
∵∠B=∠FAE,
∴∠FAE=∠ADE,
∵∠F=∠F,
∴△AEF∽△DAF,
∴$\frac{AF}{DF}$=$\frac{FE}{AF}$,
∵FA=6,FE=4,
∴DF=9.
点评 此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
6.如果2x=3y(x、y均不为0),那么下列各式中正确的是( )
| A. | $\frac{x}{y}$=$\frac{2}{3}$ | B. | $\frac{x}{x-y}$=3 | C. | $\frac{x+y}{y}$=$\frac{5}{3}$ | D. | $\frac{x}{x+y}$=$\frac{2}{5}$ |
4.下列图形中,绕着某点旋转90°后可以与原来图形重合的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.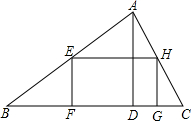 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).