题目内容
9.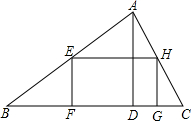 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是y=-3x2+9x(0<x<3).
分析 根据矩形性质得:EH∥BC,从而得△AEH∽△ABC,利用相似三角形对应边的比和对应高的比相等表示EH的长,利用矩形面积公式得y与x的函数解析式.
解答 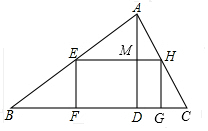 解:∵四边形EFGH是矩形,
解:∵四边形EFGH是矩形,
∴EH∥BC,
∴△AEH∽△ABC,
∴$\frac{EH}{BC}=\frac{AM}{AD}$,
∵EF=DM=x,AD=3,
∴AM=3-x,
∴$\frac{EH}{9}=\frac{3-x}{3}$,
∴EH=3(3-x)=9-3x,
∴y=EH•EF=x(9-3x)=-3x2+9x(0<x<3).
故答案为:y=-3x2+9x(0<x<3).
点评 本题考查了相似三角形的性质和判定、二次函数的关系式,熟练掌握相似三角形的性质和判定是本题的关键,注意二次函数自变量的取值.

练习册系列答案
相关题目
18. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=62°,则∠DCB的度数为( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=62°,则∠DCB的度数为( )
 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=62°,则∠DCB的度数为( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=62°,则∠DCB的度数为( )| A. | 28° | B. | 30° | C. | 59° | D. | 62° |
19.下列计算正确的是( )
| A. | (a4)3=a7 | B. | a6÷a3=a2 | C. | (2a)3=6a3 | D. | a•a3=a4 |
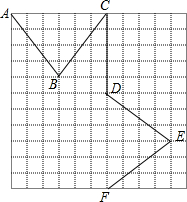 一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程)
一只小虫从A点出发,沿着图中折线到F点取食,请你计算一下,它一共走了多少路程.(写出过程) 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3.
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3.
 如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.