题目内容
16.能使$\sqrt{-(x+1)^{2}}$有意义的x值是-1;当x>4时,方程|x-4|+|x+2|=6的解为4.分析 根据二次根式有意义的条件可得-(x+1)2≥0,再解即可;根据绝对值的性质可得x-4+x+2=6,然后移项、合并同类项,把为指数的系数化为1可得x的值.
解答 解:由题意得:-(x+1)2≥0,
∴x+1=0,
解得x=-1;
∵x>4,
∴|x-4|+|x+2|=6,
x-4+x+2=6,
2x=8,
x=4,
故答案为:-1;4.
点评 此题主要考查了二次根式有意义的条件,以及一元一次方程的解法,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
13.铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为( )
| A. | 26cm | B. | 52cm | C. | 78cm | D. | 104cm |
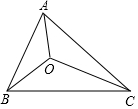 如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5.
如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5. 如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.