题目内容
2. 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F的边长=x-1
正方形E的边长=x-2,正方形C的边长=$\frac{x+1}{2}$或x-3;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN=P Q).根据等量关系可求出x=7;.
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问乙还要多少天完成?甲、乙2个工程队各铺设多少米?
分析 (1)根据图象由最小的正方形的边长为1可以得出正方形F、E和C的边长;
(2)设图中最大正方形B的边长是x米,分别表示出QM和PN的值由QM=PN建立方程求出其解即可;
(3)设余下的工程由乙队单独施工,还要y天完成,由工程问题的数量关系建立方程求出其解即可.
解答  解:(1)由题意,得
解:(1)由题意,得
正方形F的边长(x-1),
正方形E的边长(x-2),
正方形C的边长$\frac{x+1}{2}$或x-3;
故答案是:x-1;x-2;$\frac{x+1}{2}$或x-3.
(2)设图中最大正方形B的边长是x米,由图象,得
QM=x-1+x-2,PN=x+$\frac{x+1}{2}$,
∵QM=PN,
∴x-1+x-2=x+$\frac{x+1}{2}$,
∴x=7.
故答案是:7;
(3)由(1)(2)可知,长方形MNPQ的长为13米,宽为11米,则长方形MNPQ的周长为2×(13+11)=48(米).
设余下的工程由乙队单独施工,还要y天完成,由题意,得
($\frac{1}{10}$+$\frac{1}{15}$)×2+$\frac{1}{15}$y=1,
解得:y=10.
则甲工程队铺设了$\frac{2}{10}$×48=9.6(米).
乙工程队铺设了48-9.6=38.4(米).
答:还要10天完成,甲工程队铺设了9.6米,乙工程队铺设了38.4米.
点评 本题考查了代数式表示数的运用,列一元一次方程求值的运用,工程问题的数量关系的运用.在求x的值时运用矩形的性质QM=PN建立方程是关键.

练习册系列答案
相关题目
13.铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm,某厂家生产符合该规定的行李箱,已知行李箱的高为30cm,长与宽的比为3:2,则该行李箱的长的最大值为( )
| A. | 26cm | B. | 52cm | C. | 78cm | D. | 104cm |
10.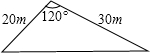 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )| A. | $450\sqrt{3}a$元 | B. | $225\sqrt{3}a$元 | C. | $150\sqrt{3}a$元 | D. | $300\sqrt{3}a$ |
11.2016年7月,河北省中南部地区出现强降雨,引发河流水势上涨,朱庄水库、临城水库和黄壁庄水库的水位都已经超过汛限,某名水库记录员在记录水位变化时,把水位上升10cm,记作+10cm,则-12cm表示( )
| A. | 水位下降12cm | B. | 水位上升12cm | C. | 水位下降6cm | D. | 水位上升6cm |
12.如图,下列图案均是长度相同的火柴按一定规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…依次规律,第12个图案需火柴棍的根数为( )


| A. | 169 | B. | 178 | C. | 183 | D. | 197 |
 如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3.
如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S△CEM等于1:3. 如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.