题目内容
18.若等腰三角形腰长为4,腰上的高为2,则此等腰三角形的底角为15或75度.分析 分该三角形为钝角三角形和锐角三角形两种情况,再结合直角三角形的性质可求得等腰三角形的顶角,再根据等腰三角形的性质可求得底角.
解答 解:
若该三角形为钝角三角形,如图1,AB=AC=4,
过B作BD⊥AC,交AC的延长线于点D,
∵BD=2,AB=4,
∴∠BAD=30°,
又AB=AC,
∴∠ABC=∠C=15°,
若该三角形为锐角三角形,如图2,AB=AC,
过B作BD⊥AC交AC于点D,
∵AB=4,BD=2,
∴∠A=30°,
又AB=AC,
∴∠ABC=∠C=$\frac{180°-30°}{2}$=75°,
综上可知该三角形的底角为15°或75°,
故答案为:15或75.
点评 本题主要考查等有腰三角形、直角三角形的性质,求得顶角的度数是解题的关键.注意分类讨论思想的应用.

练习册系列答案
相关题目
3.用一个半径为6cm的半圆围成一个圆锥的侧面,则这个圆锥的表面积为( )cm2.
| A. | 6π+6 | B. | 12π | C. | 27π | D. | 18π |
10.“寿岛血脐”是长寿湖的一种新开发的水果,而且是有很高的营养价值,某批发国商第1次共用3.9万元购进A、B两种品牌血脐,全部售完后获得利润6000元,它们的进价如下表:
(1)求该果商第一次购进A、B两种血脐各多少件;
(2)该果商第二次以原价购进A、B两种血脐,购进B种血脐的件数不变,而购进A种血脐的件数是第一次的2倍,A种血脐按原价销售,而B种血脐打折销售,若两种血脐销售完毕,要使得第二次经营活动或利润不少于7500元,求B种血脐最低售价是多少?
| 型 号 | A | B |
| 进价(元/件) | 120 | 100 |
| 售价(元/件) | 135 | 120 |
(2)该果商第二次以原价购进A、B两种血脐,购进B种血脐的件数不变,而购进A种血脐的件数是第一次的2倍,A种血脐按原价销售,而B种血脐打折销售,若两种血脐销售完毕,要使得第二次经营活动或利润不少于7500元,求B种血脐最低售价是多少?
7.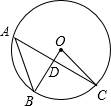 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )| A. | 80° | B. | 60° | C. | 50° | D. | 40° |
8.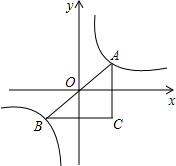 A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
 A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )
A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点,AC∥y轴,BC∥x轴,则△ABC的面积S为( )| A. | S=1 | B. | 1<S<2 | C. | S=2 | D. | S>2 |

