题目内容
8．
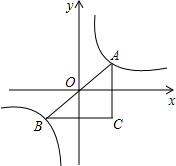A、B两点是反比例函数y=$\frac{1}{x}$的图象上关于原点对称的两点，AC∥y轴，BC∥x轴，则△ABC的面积S为（ ）| A． | S=1 | B． | 1＜S＜2 | C． | S=2 | D． | S＞2 |
分析 连接OC，设AC与x轴交于点D，BC与y轴交于点E．首先由反比例函数y=$\frac{k}{x}$的比例系数k的几何意义，可知△AOD的面积等于$\frac{1}{2}$|k|，再由A、B两点关于原点对称，BC∥x轴，AC∥y轴，可知S△AOC=2×S△AOD，S△ABC=2×S△AOC，从而求出结果．
解答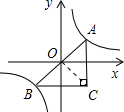 
解：如图，连接OC，设AC与x轴交于点D，BC与y轴交于点E．
∵A、B两点关于原点对称，BC∥x轴，AC∥y轴，
∴AC⊥x轴，AD=CD，OA=OB．
∴S△COD=S△AOD=$\frac{1}{2}$，
∴S△AOC=1，
∴S△BOC=S△AOC=1，
∴S△ABC=S△BOC+S△AOC=2．
故选C．
点评 本题主要考查了三角形一边上的中线将三角形的面积二等分及反比例函数的比例系数k的几何意义：反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系，即S=$\frac{1}{2}$|k|．
练习册系列答案
阅读快车系列答案
相关题目
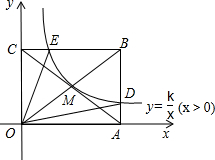如图，反比例函数$y=\frac{k}{x}（{x＞0}）$的图象经过矩形OABC对角线的交点M，分别与AB、BC相交于点D、E，若四边形ODBE的面积为12，则k的值为4．
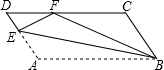如图，在?ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F处．若△FDE的周长为5，△FCB的周长为17，则FC的长为6．
在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=$\frac{3}{5}$，反比例函数y=$\frac{k}{x}$（k＞0）的图象经过AO的中点C且与AB交于点D．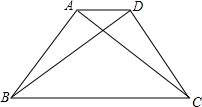
如图，在梯形ABCD中，AD∥BC，AC⊥BD，AD=1，AC=3，BD=4，求BC的长及梯形ABCD的面积．