题目内容
13.如图,AB∥CD,分别探讨下面四个图形中∠A与∠P、∠C的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线)
分析 在图(1)(2)中可过P作平行线,根据平行线的性质可求得∠A与∠P、∠C的关系;在(3)中根据平行线的性质和三角形内角和定理可求得∠A与∠P、∠C的关系;在(4)中延长BA交PC于点E,利用平行线的性质和三角形外角的性质可求得∠A与∠P、∠C的关系.
解答  解:(1)∠P=∠A+∠C,(2)∠A+∠P+∠C=360°,(3)∠C=∠A+∠P,(4)∠A=∠P+∠C.
解:(1)∠P=∠A+∠C,(2)∠A+∠P+∠C=360°,(3)∠C=∠A+∠P,(4)∠A=∠P+∠C.
选(3)证明如下:
如图(3),设AB、PC交于点E,
∵AB∥CD,
∴∠PEB=∠C,
又∵∠PEB=∠A+∠P,
∴∠C=∠A+∠P.
点评 本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | x3+x2=x5 | B. | m3÷m3=m | C. | 3x+3y=6xy | D. | (a3)3=a9 |
5.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{9x}$ | B. | $\sqrt{x-2}$ | C. | $\sqrt{\frac{x-y}{x}}$ | D. | $\sqrt{3{a}^{2}b}$ |
 如图,双曲线y=$\frac{6}{x}$与y=$\frac{2}{x}$在第一象限内的图象依次是m和n,设点P在图象m上,PC⊥x轴,PD⊥y轴,则四边形PAOB的面积为4.
如图,双曲线y=$\frac{6}{x}$与y=$\frac{2}{x}$在第一象限内的图象依次是m和n,设点P在图象m上,PC⊥x轴,PD⊥y轴,则四边形PAOB的面积为4.
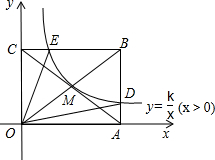 如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.
如图,反比例函数$y=\frac{k}{x}({x>0})$的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,若四边形ODBE的面积为12,则k的值为4.