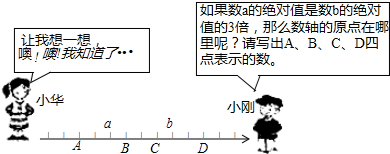
题目内容
在Rt△ABC中，斜边BC2=2，则AB2+BC2+AC2的值为 ．
考点：勾股定理
专题：
分析：利用勾股定理将AB2+AC2转化为BC2，再求值．
解答：解：∵Rt△ABC中，BC为斜边，
∴AB2+AC2=BC2，
∴AB2+BC2+AC2=2BC2=2×2=4．
故答案为：4．
∴AB2+AC2=BC2，
∴AB2+BC2+AC2=2BC2=2×2=4．
故答案为：4．
点评：本题考查了勾股定理．正确判断直角三角形的直角边、斜边，利用勾股定理得出等式是解题的关键．
练习册系列答案
相关题目
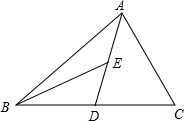如图，AD为△ABC的中线，BE为△ABD的角平分线．
如图，已知弦AB、CD相交于P点，且∠AOC=44°，∠BOD=46°．则∠APC的度数是
如图，在△ABC中，AD⊥BC，AE平分∠BAC，完成下列问题：
如图，在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为（6，0），点B的坐标为（3，4），点C在y轴的正半轴上．动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）．