题目内容
已知等腰三角形的两边长为7和4,周长为奇数,求三角形周长.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:已知等腰三角形的两边长分别为一奇数一偶数,且周长为奇数,所以另一边一定为一偶数,从而可得到腰长的值,从而不难求解.
解答:解:∵等腰三角形的两边长分别为7和4,且周长为奇数,
∴第三边一定为偶数,
∴腰长为4,
∴周长=4+4+7=15.
∴第三边一定为偶数,
∴腰长为4,
∴周长=4+4+7=15.
点评:此题主要考查等腰三角形的性质及三角形三边关系的综合运用,关键是确定哪边为腰长.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
下列结论中正确的是( )
| A、字母a表示任意数 | ||||
B、-
| ||||
| C、x-y=3是代数式 | ||||
| D、a不是代数式 |
 如图,已知棋子“卒”的坐标为 (-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
如图,已知棋子“卒”的坐标为 (-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )| A、(2,2) |
| B、(4,1) |
| C、(-2,2) |
| D、(4,2) |
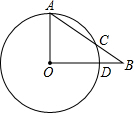 如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长.
如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长. 图示,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是
图示,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是