题目内容
如图1,△BAC和△DAE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连BD、CE.

(1)求证:BD=CE;
(2)如图2,延长BD交CE于F,连AF,求∠AFB的度数.

(1)求证:BD=CE;
(2)如图2,延长BD交CE于F,连AF,求∠AFB的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)求出∠BAD=∠CAE,根据SAS推出△BAD≌△CAE即可;
(2)根据全等求出∠ACE=∠ABD,求出∠CFO=∠BAO=90°,推出D、A、E、F四点共圆,求出∠AFB=∠DEA,即可求出答案.
(2)根据全等求出∠ACE=∠ABD,求出∠CFO=∠BAO=90°,推出D、A、E、F四点共圆,求出∠AFB=∠DEA,即可求出答案.
解答:(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE=90°-∠CAD,
在△BAD和△CAE中
∴△BAD≌△CAE,
∴BD=CE;

(2)解:∵△BAD≌△CAE,
∴∠ACE=∠ABD,
∵∠COF=∠AOB,∠OCF+∠CFO+∠COF=180°,∠ABD+∠AOB+∠OAB=180°,∠BAO=90°,
∴∠CFO=∠BAO=90°,
∴∠OFE=90°,
∵∠DAE=90°,
∴∠DFE+∠DAE=180°,
∴D、A、E、F四点共圆,
∴∠AFB=∠DEA,
∵在△ADE中,∠DAE=90°,AD=AE,
∴∠DEA=45°,
∴∠AFB=45°.
∴∠BAD=∠CAE=90°-∠CAD,
在△BAD和△CAE中
|
∴△BAD≌△CAE,
∴BD=CE;

(2)解:∵△BAD≌△CAE,
∴∠ACE=∠ABD,
∵∠COF=∠AOB,∠OCF+∠CFO+∠COF=180°,∠ABD+∠AOB+∠OAB=180°,∠BAO=90°,
∴∠CFO=∠BAO=90°,
∴∠OFE=90°,
∵∠DAE=90°,
∴∠DFE+∠DAE=180°,
∴D、A、E、F四点共圆,
∴∠AFB=∠DEA,
∵在△ADE中,∠DAE=90°,AD=AE,
∴∠DEA=45°,
∴∠AFB=45°.
点评:此题考查了全等三角形的判定和性质,三角形内角和定理,圆内接四边形的性质的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
等腰三角形的两边分别为6cm、4cm,则它的周长是( )
| A、14cm |
| B、16cm或14cm |
| C、16cm |
| D、18cm |
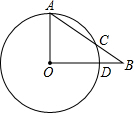 如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长.
如图,在Rt△AOB中,∠AOB=90°,以OA为半径的圆交AB于点C.若AO=5,OB=12,求BC的长. 如图,△ABC中,BE平分∠ABC,DE∥BC交于AB于点D,BC=6,AB=9,求DE的长.
如图,△ABC中,BE平分∠ABC,DE∥BC交于AB于点D,BC=6,AB=9,求DE的长.