题目内容
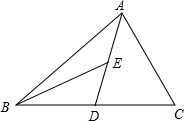 如图,AD为△ABC的中线,BE为△ABD的角平分线.
如图,AD为△ABC的中线,BE为△ABD的角平分线.(1)若∠BED=40°,∠BAD=25°,求∠ABD的度数;
(2)在△BED中作BD边上的高EM;
(3)在(1)的条件下,若△ABC的面积为40,BD=5,求EM的长.
考点:三角形的角平分线、中线和高,三角形的面积,三角形内角和定理
专题:
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ABE,再根据角平分线的定义可得∠ABD=2∠ABE;
(2)根据三角形的高线的定义作出即可;
(3)过点A作AF⊥BC于F,过点E作EN⊥AB于N,利用三角形的面积求出AF,根据直角三角形30°角所对的直角边等于斜边的一半求出AB,再根据角平分线上的点到角的两边距离相等可得EM=EN,然后利用△ABD的面积列式计算即可得解.
(2)根据三角形的高线的定义作出即可;
(3)过点A作AF⊥BC于F,过点E作EN⊥AB于N,利用三角形的面积求出AF,根据直角三角形30°角所对的直角边等于斜边的一半求出AB,再根据角平分线上的点到角的两边距离相等可得EM=EN,然后利用△ABD的面积列式计算即可得解.
解答: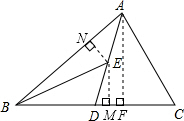 解:(1)∵∠BED=40°,∠BAD=25°,
解:(1)∵∠BED=40°,∠BAD=25°,
∴∠ABE=∠BED-∠BAD=40°-25°=15°,
∵BE为△ABD的角平分线,
∴∠ABD=2∠ABE=2×15°=30°;
(2)高EM如图所示;
(3)过点A作AF⊥BC于F,过点E作EN⊥AB于N,
∵BD=5,AD为△ABC的中线,
∴BC=2BD=2×5=10,
∴△ABC的面积=
×10×AF=40,
解得AF=8,
∴AB=2AF=2×8=16,
∵BE为△ABD的角平分线,
∴EM=EN,
∴△ABD的面积=
×(16+5)×EM=
×5×8,
解得EM=
.
 解:(1)∵∠BED=40°,∠BAD=25°,
解:(1)∵∠BED=40°,∠BAD=25°,∴∠ABE=∠BED-∠BAD=40°-25°=15°,
∵BE为△ABD的角平分线,
∴∠ABD=2∠ABE=2×15°=30°;
(2)高EM如图所示;
(3)过点A作AF⊥BC于F,过点E作EN⊥AB于N,
∵BD=5,AD为△ABC的中线,
∴BC=2BD=2×5=10,
∴△ABC的面积=
| 1 |
| 2 |
解得AF=8,
∴AB=2AF=2×8=16,
∵BE为△ABD的角平分线,
∴EM=EN,
∴△ABD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
解得EM=
| 40 |
| 21 |
点评:本题考查了三角形的角平分线、中线和高,三角形的面积,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键,难点在于(3)利用△ABD的面积列出方程.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
实数
,π,
,
,-
中,有理数有( )
| 2 |
| 5 |
| 9 |
| 13 |
| 3 | 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
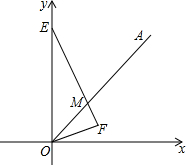 如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF.
如图,OA为第一象限的角平分线,点E在y轴上,∠OEF=∠AOF,FE⊥OF交OA于M点.求证:EM=2OF. 如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F,延长CE到点G,使CG=AB,若∠BCE=45°,求证:点F、点G关于AB对称.
如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F,延长CE到点G,使CG=AB,若∠BCE=45°,求证:点F、点G关于AB对称.