题目内容
15. 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
分析 延长DM交AB于N,由翻折性质得∠C=∠AMD=90°,根据角平分线的定义得到∠DAM=∠NAM,推出△ADM≌△ANM,得到DM=MN,于是得到S△AMB=$\frac{1}{2}$S△ABD=$\frac{1}{2}$BD•AC=$\frac{1}{2}$×10×8=40,
解答 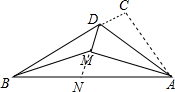 解:延长DM交AB于N,由翻折性质得:∠C=∠AMD=90°,
解:延长DM交AB于N,由翻折性质得:∠C=∠AMD=90°,
∵MA平分∠BAD,
∴∠DAM=∠NAM,
在△ADM和△ANM中,
$\left\{\begin{array}{l}{∠AMD=∠AMN=90°}\\{AM=AM}\\{∠DAM=∠NAM}\end{array}\right.$,
∴△ADM≌△ANM,
∴DM=MN,
∴S△AMN=$\frac{1}{2}$S△ADN,S△BMN=$\frac{1}{2}$S△BDN,
∴S△AMB=$\frac{1}{2}$S△ABD=$\frac{1}{2}×$$\frac{1}{2}$BD•AC=$\frac{1}{2}×$$\frac{1}{2}$×10×8=20.
故答案为:20.
点评 本题考查了翻折变换-折叠问题,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20.下列命题为真命题的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 在同圆或等圆中、相等的弦所对的圆周角相等 | |
| C. | 平分弦所对的一条弧的直径一定垂直平分这条弦 | |
| D. | 相等的圆心角所对的弧相等,所对的弦也相等 |
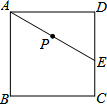 如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.
如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于60°或120°.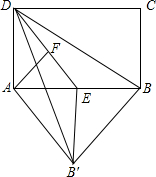 在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.
在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.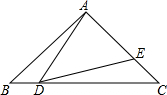 如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;
如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;