题目内容
5.因式分解:m3-9m=m(m+3)(m-3).分析 原式提取m,再利用平方差公式分解即可.
解答 解:原式=m(m2-9)
=m(m+3)(m-3),
故答案为:m(m+3)(m-3).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -x6÷x2=-x4 | C. | 2x+2y=4xy | D. | (x-1)2=x2-12 |
20.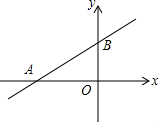 如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
 如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
17. 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
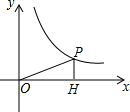 如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$.
如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$.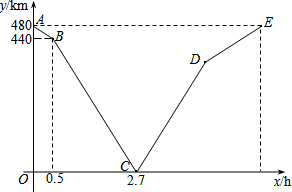 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题: 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.