题目内容
7.计算.(1)$\frac{1}{\sqrt{2}-1}$-$\sqrt{12}$-($\sqrt{2}$+1)2+$\sqrt{\frac{3}{4}}$;
(2)($\sqrt{3}$+$\sqrt{2}$-1)($\sqrt{3}$-$\sqrt{2}$+1)
(3)(5$\sqrt{2}$+4$\sqrt{3}$)(5$\sqrt{2}$-4$\sqrt{3}$)2.
分析 (1)首先化简二次根式,进而合并同类二次根式即可;
(2)首先化简二次根式,进而利用二次根式的乘法运算法则求出即可;
(3)首先化简二次根式,进而利用二次根式的乘法运算法则求出即可.
解答 解:(1)$\frac{1}{\sqrt{2}-1}$-$\sqrt{12}$-($\sqrt{2}$+1)2+$\sqrt{\frac{3}{4}}$
=$\sqrt{2}$+1-2$\sqrt{3}$-(3+2$\sqrt{2}$)+$\frac{\sqrt{3}}{2}$
=-$\sqrt{2}$-$\frac{3\sqrt{3}}{2}$-2;
(2)($\sqrt{3}$+$\sqrt{2}$-1)($\sqrt{3}$-$\sqrt{2}$+1)
=[$\sqrt{3}$+($\sqrt{2}$-1)][$\sqrt{3}$-($\sqrt{2}$-1)]
=($\sqrt{3}$)2-($\sqrt{2}$-1)2
=3-(3-2$\sqrt{2}$)
=2$\sqrt{2}$;
(3)(5$\sqrt{2}$+4$\sqrt{3}$)(5$\sqrt{2}$-4$\sqrt{3}$)2
=[(5$\sqrt{2}$)2-(4$\sqrt{3}$)2](5$\sqrt{2}$-4$\sqrt{3}$)
=2(5$\sqrt{2}$-4$\sqrt{3}$)
=10$\sqrt{2}$-8$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
17. 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
2.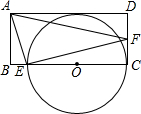 如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
 如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )
如图,矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,以EC为直径的⊙O与AD相切,则tan∠AFE的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
12.如果一个多边形的每一个内角都相等,且每一个内角的度数为135°,那么这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 以上答案都不对 |
19.下列函数是一次函数但不是正比例函数的是( )
| A. | y=-$\frac{1}{x}$ | B. | y=x2 | C. | y=x | D. | y=$\frac{x+1}{2}$ |
16.下列各式中,是分式的是( )
| A. | $\frac{{x}^{2}+1}{2}$ | B. | $\frac{3xy}{π}$ | C. | $\frac{3}{xy}$ | D. | $\frac{m-n}{5}$ |
 郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.
郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示. 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.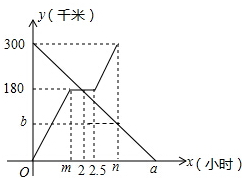 甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.