题目内容
18.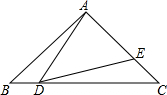 如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;
如图.在△ABC中.AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE;(1)运动3秒时,AE=$\frac{1}{2}$DC(不必说明理由);
(2)运动多少秒时,∠ADE=∠B,并请说明理由.
分析 (1)设运动的时间是t秒,则CD=12-2t,AE=9-2t,得出方程9-2t=$\frac{1}{2}$(12-2t),求出方程的解即可;
(2)求出∠B=∠C=∠ADE,推出∠BAD=∠EDC,根据AAS证△ABD≌△DCE,推出DC=AB=9即可.
解答 解:(1)设运动的时间是t秒,
则CD=12-2t,AE=9-2t,
9-2t=$\frac{1}{2}$(12-2t)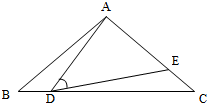
t=3,
故答案为:3.
(2)设x秒后,∠ADE=∠B,
∵∠B=∠C=90°-$\frac{1}{2}$∠BAC,
∴∠B=∠C=∠ADE,
∵∠BAD+∠ADB+∠B=180°,∠EDC+∠ADE+∠ADB=180°,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BAD=∠CDE}\\{BD=CE}\end{array}\right.$
∴△ABD≌△DCE(AAS),
∴DC=AB=9,
∴BD=3,
∴x=$\frac{3}{2}$,
即运动$\frac{3}{2}$秒时,∠ADE=90°-$\frac{1}{2}$∠BAC,
∵AB=AC=9cm,
∴∠B=∠C=$\frac{180°-∠BAC}{2}$,
即∠B=90°-$\frac{1}{2}$∠BAC,
∵∠ADE=90°-$\frac{1}{2}$∠BAC,
∴∠ADE=∠B.
点评 本题考查了全等三角形的性质和判定,三角形的内角和定理,等腰三角形的性质,利用了三角形内角和定理,得出方程是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各式中,是分式的是( )
| A. | $\frac{{x}^{2}+1}{2}$ | B. | $\frac{3xy}{π}$ | C. | $\frac{3}{xy}$ | D. | $\frac{m-n}{5}$ |
7.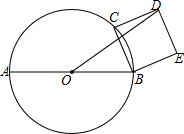 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
 如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )
如图,AB为⊙O的直径,AB=4,点C为半圆AB上动点,以BC为边在⊙O外作正方形BCDE,(点D在直线AB的上方)连接OD.当点C运动时,则线段OD的长( )| A. | 随点C的运动而变化,最大值为2+2$\sqrt{2}$ | B. | 不变 | ||
| C. | 随点C的运动而变化,最大值为2$\sqrt{2}$ | D. | 随点C的运动而变化,但无最值 |
 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.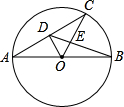 如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.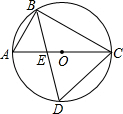 如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.
如图.AC是⊙O的直径,点B在⊙O上,∠ACB=30°.作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD,求△ABE与△CDE的面积之比.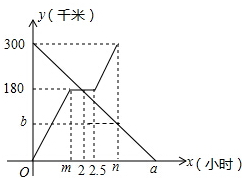 甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.