题目内容
3.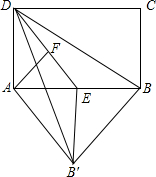 在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.
在矩形ABCD中,E为AB边上的中点,将△BDE翻折,B的对应点记为B′,已知AD=4,AB=6,F为线段DE上一动点,当∠DAF=∠BAB′时,则DF+BB′=8.
分析 根据勾股定理得到DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=5,BD=$\sqrt{A{D}^{2}+B{A}^{2}}$=$\sqrt{52}$,根据折叠的性质得到BE=B′E,BD=B′D,由直角三角形的判定得到∠AB′B=90°,推出AF∥BB′,延长DE交BB′于H,得到DH垂直平分BB′,设BH=x,EH=y,列方程组得到BB′=$\frac{24}{5}$,根据射影定理得到DF=$\frac{A{D}^{2}}{DE}$=$\frac{16}{5}$,即可得到结论.
解答 解:在矩形ABCD中,E为AB边上的中点,AD=4,AB=6,
∴AE=$\frac{1}{2}$AB=3,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=5,BD=$\sqrt{A{D}^{2}+B{A}^{2}}$=$\sqrt{52}$,
∵将△BDE翻折,B的对应点记为B′,
∴BE=B′E,BD=B′D,
∴B′E=$\frac{1}{2}$AB,
∴∠AB′B=90°,
∵∠DAF=∠BAB′,
∴∠B′AF=∠DAB=90°,
∴AF∥BB′,
延长DE交BB′于H,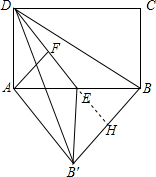
∴DH垂直平分BB′,
设BH=x,EH=y,
∴$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=9}\\{(5+y)^{2}+{x}^{2}=52}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{12}{5}}\\{y=\frac{9}{5}}\end{array}\right.$,
∴BB′=$\frac{24}{5}$,
∵AF∥BB′,
∴AF⊥DH,
∴DF=$\frac{A{D}^{2}}{DE}$=$\frac{16}{5}$,
∴DF+BB′=$\frac{16}{5}$+$\frac{24}{5}$=8.
故答案为:8.
点评 本题考查了翻折变换-折叠问题,矩形的性质,勾股定理,平行线的判定和性质,熟练掌握折叠的性质是解题的关键.

| A. | (2a2)3=6a6 | B. | -x6÷x2=-x4 | C. | 2x+2y=4xy | D. | (x-1)2=x2-12 |
| A. | b3•b4=b7 | B. | (b3)4=b7 | C. | b3+b4=b7 | D. | b6÷b3=b2 |
| A. | 6 | B. | 7 | C. | 8 | D. | 以上答案都不对 |
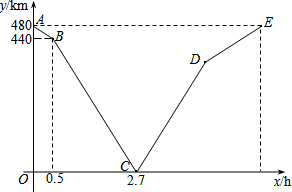 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题: 郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示.
郑州市北环彩虹桥在上下班高峰期经常堵车,交通管理部门为了解交通拥堵情况,进行了统计分析,桥上的车流速度v(km/h)关于车流密度x(辆/km)的函数图象如图所示. 如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数.
如图,已知AB∥CD,∠BAE=3∠ECF,∠ECF=28°,求∠E的度数. 如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.
如图,已知Rt△ABC中,∠C=90°,∠C沿AD对折得∠AMD,MA平分∠BAD,连接MB,其中AC=8,BD=10,△ABM的面积是20.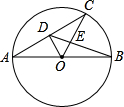 如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.
如图,AB为⊙O的直径,AC为弦,OD⊥AC于点D,BD交OC于点E,若AC=4,AB=5,则BE=$\frac{2\sqrt{13}}{3}$.