题目内容
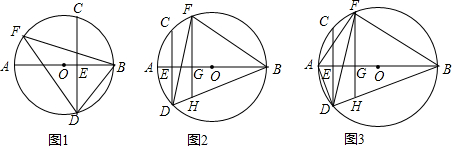
13.已知:AB为⊙O的直径,弦CD⊥AB于点E,F为⊙O上一点,且FB=FD.(1)如图1,点F在弧AC上时,求证:∠BDC=∠DFB;
(2)如图2,点F在弧BC上时,过点F作FH∥CD分别交AB、BD于点G、H,求证:BD=2FG;
(3)如图3,在(2)的条件下,连接AD、AF,DH:HG=3:5,OG=5,求△ADF的面积.
分析 (1)由AB为⊙O的直径,弦CD⊥AB,根据垂径定理的即可证得$\widehat{BC}$=$\widehat{BD}$,然后由圆周角定理,证得:∠BDC=∠DFB;
(2)首先连接FO并延长交BD于点M,连接OD,易证得△FOD≌△FOB(SSS),证得BM=DM=$\frac{1}{2}$BD,继而证得△FGB≌△BMF(AAS),则可证得结论;
(3)首先设DH=3m,GH=5m,易证得△FHM≌△BHG(AAS),然后由勾股定理得方程(12m-5)2=(8m)2+52,解此方程即可求得答案.
解答 (1)证明:∵AB为⊙O的直径,弦CD⊥AB,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠BDC=∠DFB;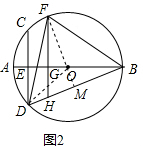 (2)证明:如图2,连接FO并延长交BD于点M,连接OD,
(2)证明:如图2,连接FO并延长交BD于点M,连接OD,
在△FOD和FOB中,
$\left\{\begin{array}{l}{OF=OF}\\{FD=FB}\\{OD=OB}\end{array}\right.$,
∴△FOD≌△FOB(SSS),
∴∠DFO=∠BFO,
∵FD=FB,
∴FM⊥BD,
∴BM=DM=$\frac{1}{2}$BD,
∵OF=OB,
∴∠OFB=∠OBF,
∵FH∥CD,
∴∠CEG=∠FGB=90°,
在△FGB和△FBM中,
$\left\{\begin{array}{l}{∠FMB=∠BGF}\\{∠MFB=∠GBF}\\{FB=FB}\end{array}\right.$,
∴△FGB≌△BMF(AAS),
∴FG=BM,
∴BD=2FG;
(3)解:如图3,∵DH:HG=3:5,
∴设DH=3m,GH=5m,
∵△FGB≌△BMF,
∴FM=BG,
在△FHM和△BHG中,
$\left\{\begin{array}{l}{∠FHB=∠BHG}\\{∠BGH=∠FMH}\\{FM=BG}\end{array}\right.$,
∴△FHM≌△BHG(AAS),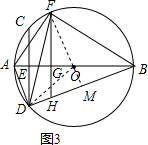 ∴HM=GH=5m,DM=8m,BH=13m,
∴HM=GH=5m,DM=8m,BH=13m,
在Rt△BGH中,HB=13m,GH=5m,
由勾股定理得:GB=12m,
在Rt△FGO中,FG=8m,OG=5,OF=OB=12m-5,
∵FG2+OG2=OF2,
∴(12m-5)2=(8m)2+52,
解得:m1=$\frac{3}{2}$,m2=0(舍去);
∴OB=24,DM=12,OF=OB=13,AB=26,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=10,
∴S△ADF=$\frac{1}{2}$×AD×DM=60.
点评 此题属于圆的综合题,考查了圆周角定理、垂径定理、全等三角形的判定与性质以及勾股定理等知识.注意准确作出辅助线是解此题的关键.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 已知:抛物线l1:y=-x2+bx+3交x轴于点A,B(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,-$\frac{5}{2}$).
已知:抛物线l1:y=-x2+bx+3交x轴于点A,B(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,-$\frac{5}{2}$).
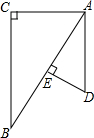 如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在线段AB上,AD∥CB,若AC=AE=2,BC=3,则DE的长为$\frac{4}{3}$.
如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在线段AB上,AD∥CB,若AC=AE=2,BC=3,则DE的长为$\frac{4}{3}$.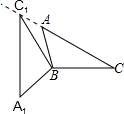 如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.
如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.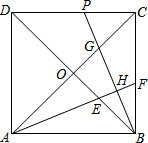 已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.
已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.