题目内容
3. 已知:抛物线l1:y=-x2+bx+3交x轴于点A,B(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,-$\frac{5}{2}$).
已知:抛物线l1:y=-x2+bx+3交x轴于点A,B(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,-$\frac{5}{2}$).(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标.
分析 (1)利用对称轴公式求得b的值,即得到抛物线l1的解析式,然后根据解析式求得点A的坐标,所以利用点A、点E、点D的坐标来求抛物线l2的函数表达式;
(2)设P(1,y),由(1)可得C(0,3).利用两点间的距离公式进行解答即可.
解答 解:(1)∵抛物线l1:y=-x2+bx+3的对称轴为x=1,
∴-$\frac{b}{-2}$=-1,
解得b=2,
∴抛物线l1的解析式为:y=-x2+2x+3,或者y=-(x-1)(x+3),
∴点A的坐标是(-1,0).
又∵抛物线l2经过点A,与x轴的另一个交点为E(5,0),
∴可设抛物线l2的解析式为:y=a(x+1)(x-5),
又∵抛物线l2经过点D(0,-$\frac{5}{2}$),
∴-5a=-$\frac{5}{2}$,
解得a=$\frac{1}{2}$.
则抛物线l2的函数表达式为:y=$\frac{1}{2}$(x+1)(x-5)或y=$\frac{1}{2}$x2-2x-$\frac{5}{2}$;
(2)设P(1,y),由(1)可得C(0,3).
∴PC2=12+(y-3)2=y2-6y+10,PA2=[1-(-1)]2+y2=4+y2.
∵PA=PC,
∴y2-6y+10=4+y2,
解得y=1.
∴点P的坐标是P(1,1).
点评 本题考查了抛物线与x轴的交点坐标.二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
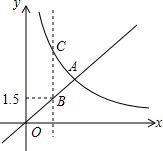 已知函数y1=x(x>0),y2=$\frac{9}{x}$(x>0)的图象如图,有下列结论:
已知函数y1=x(x>0),y2=$\frac{9}{x}$(x>0)的图象如图,有下列结论: 如图,与∠CAB成内错角的是∠HCA,∠ABI.
如图,与∠CAB成内错角的是∠HCA,∠ABI.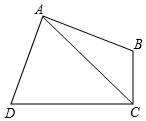 如图,四边形ABCD中,∠A=∠C=90度,AB=AD,若这个四边形的面积为24,则AC的长是4$\sqrt{3}$.
如图,四边形ABCD中,∠A=∠C=90度,AB=AD,若这个四边形的面积为24,则AC的长是4$\sqrt{3}$.