��Ŀ����
4����ͼ1������ABCD�У�AD��BC��AB=AD=DC=5��BC=11��һ������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ����߶�BC�����˶�������P��PQ��BC�������߶�BA-AD�ڵ�Q����PQΪ��������������PQMN����N������BC�ϣ���Q�㵽��D��ʱ���˶����������P���˶�ʱ��Ϊt�루t��0������1����������PQMN�ı�MNǡ�þ�����Dʱ�����˶�ʱ��t��ֵ��
��2���������˶������У���������PQMN���BCD���غϲ������ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
��3����ͼ2������Q���߶�AD���˶�ʱ���߶�PQ��Խ���BD���ڵ�E������DEQ��BD���ۣ��õ���DEF������PF���Ƿ����������t��ʹ��PEF�ǵ��������Σ������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
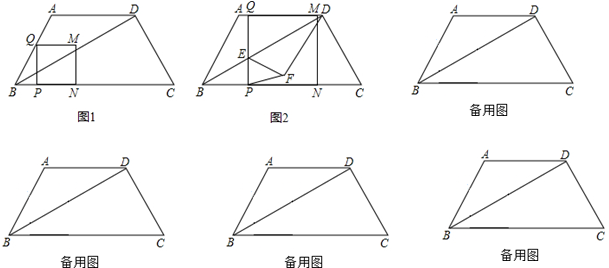
���� ��1������ı��ʾ�����BP�ij��ȣ���������PQMN�ı�MNǡ�ù���Dʱ����M���D�غϣ���ʱMQ=4����AG��BC��G��DH��BC��H����GP=AQ=AD-DQ=1��BP=BG+GP=4����t=4��
��2�������������0��t��3��3��t��4��4��t��7��7��t��8������ÿһ�������������ʾ��ͼ��ȷ���ص����ֵ���״���ټ��������
��3�������������EF=EP��FE=FP��PE=PF��ͬ��������ÿһ�������������Ӧͼ�Σ��з�����⣮
��� �⣺��1����ͼ2����AG��BC��G��DH��BC��H�����ı���AGHD�Ǿ��Σ�
������ABCD��AB=AD=DC=5��
���ABG�ա�DCH��
��BG=$\frac{1}{2}$��BC-AD��=3��AG=4��
�൱������PQMN�ı�MNǡ�ù���Dʱ����M���D�غϣ���ʱMQ=4��
GP=AQ=AD-DQ=1��BP=BG+GP=4��
�൱t=4ʱ��������PQMN�ı�MNǡ�ù���D��
��2����ͼ1����0��t��3ʱ��BP=t��
��tan��DBC=$\frac{1}{2}$��tan��C=tan��ABC=$\frac{4}{3}$��
��GP=$\frac{1}{2}$t��PQ=$\frac{4}{3}$t��BN=t+$\frac{4}{3}$t=$\frac{7}{3}$t��NR=$\frac{7}{6}$t��
��$S=\frac{\frac{4}{3}t��\frac{1}{2}t+\frac{7}{6}t��}{2}=\frac{10}{9}{t}^{2}$��
��ͼ3����3��t��4ʱ��
BP=t��GP=$\frac{1}{2}$t��PQ=4��BN=t+4��NR=$\frac{1}{2}$t+2��
��$S=\frac{��\frac{1}{2}t+\frac{1}{2}t+2����4}{2}=2t+4$��
ͼ4����4��t��7ʱ��
BP=t��GP=$\frac{1}{2}$t��PQ=4��PH=8-t��BN=t+4��HN=t+4-8=t-4��
��CN=3-��t-4��=7-t��NR=$\frac{28-4t}{3}$��
��S=$\frac{��\frac{1}{2}t+4����8-t��}{2}+\frac{��\frac{28-4t}{3}+4����t-4��}{2}$=$-\frac{11}{12}{t}^{2}+\frac{28}{3}t-\frac{32}{3}$��
��ͼ5����7��t��8ʱ��
BP=t��GP=$\frac{1}{2}$t��PQ=4��PH=8-t��
��$S=\frac{��\frac{1}{2}t+4������8-t��}{2}$+$\frac{3��4}{2}$=$-\frac{1}{4}{t}^{2}$+22��
������������$S=\left\{\begin{array}{l}{\frac{10}{9}{t}^{2}��0��t��3��}\\{2t+4��3��t��4��}\\{-\frac{11}{12}{t}^{2}+\frac{28}{3}t-\frac{32}{3}��4��t��7��}\\{-\frac{1}{4}{t}^{2}+22��7��t��8��}\end{array}\right.$
��3���ߡ�PEF+��QEF=180��=��QDF+��QEF��
���PEF=��QDF=2��ADB=��ABC��
��cos��ABC=cos��PEF=$\frac{3}{5}$��
�ɣ�1����֪EP=$\frac{1}{2}$BP=$\frac{1}{2}$t����EF=EQ=PQ-EP=4-$\frac{1}{2}$t��
��ͼ6����EF=EPʱ��
$4-\frac{1}{2}t=\frac{1}{2}t$��
��t=4��
��ͼ7����FE=FPʱ��
��FR��EP��R��
��ER=$\frac{1}{2}$EP=$\frac{3}{5}$EF��
��$\frac{1}{2}•\frac{1}{2}t=\frac{3}{5}��4-\frac{1}{2}t��$��
��$t=\frac{48}{11}$��
��ͼ8����PE=PFʱ��
��PS��EF��S��
��ES=$\frac{1}{2}$EF=$\frac{3}{5}$PE��
��$\frac{1}{2}��4-\frac{1}{2}t��=\frac{3}{5}•\frac{1}{2}t$��
��$t=\frac{40}{11}$��
������������t=4��$\frac{40}{11}$��$\frac{48}{11}$ʱ����PEF�ǵ��������Σ�
���� �������ı����ۺ��⣬Ҳ�Ƕ�̬����ѹ���⣬��Ҫ���������ε����ʡ�ȫ�������ε��ж������ʡ����ε��ж������ʡ����������ε��ж������ʡ���������������������ε��ж������ʵ�֪ʶ�㣬�ۺ��Ժ�ǿ���ѶȽϴ�������˼�뼰����˼�������Ӧ���ǽ����Ĺؼ���

 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�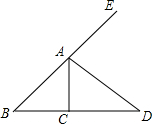 ��ͼ��AD�ǡ�CAE��ƽ���ߣ���B=35�㣬��DAE=60�㣬���ACD=��������
��ͼ��AD�ǡ�CAE��ƽ���ߣ���B=35�㣬��DAE=60�㣬���ACD=��������| A�� | 25�� | B�� | 85�� | C�� | 60�� | D�� | 95�� |
 ��ͼ�����CAB���ڴ��ǵ��ǡ�HCA����ABI��
��ͼ�����CAB���ڴ��ǵ��ǡ�HCA����ABI��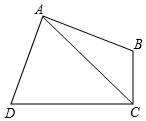 ��ͼ���ı���ABCD�У���A=��C=90�ȣ�AB=AD��������ı��ε����Ϊ24����AC�ij���4$\sqrt{3}$��
��ͼ���ı���ABCD�У���A=��C=90�ȣ�AB=AD��������ı��ε����Ϊ24����AC�ij���4$\sqrt{3}$��