题目内容
11. 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?步骤:
1.设长为xm,透光面积为ym2先列出函数解析式S=-$\frac{2}{3}$x2+$\frac{8}{3}$x;
2.求出自变量x的取值范围0<x<4;
3.利用解析式求函数的最值并思考最大透光面积能在自变量取值范围内取到吗?
分析 (1)设窗的高度为xm,宽为($\frac{8-2x}{3}$)m,根据矩形面积公式列出二次函数关系式;
(2)根据长宽均为正数,列不等式组即可解答;
(3)利用二次函数性质求出最值,再考虑取值范围即可.
解答 解:(1)设窗的高度为xm,宽为($\frac{8-2x}{3}$)m,
故S=$\frac{x(8-2x)}{3}$=-$\frac{2}{3}$x2+$\frac{8}{3}$x.
故答案为:S=-$\frac{2}{3}$x2+$\frac{8}{3}$x.
(2)根据题意x满足$\left\{\begin{array}{l}{x>0}\\{\frac{8-2x}{3}>0}\end{array}\right.$,
解得:0<x<4.
故答案为:0<x<4;
(3)∵S=-$\frac{2}{3}$x2+$\frac{8}{3}$x=-$\frac{2}{3}$(x-2)2+$\frac{8}{3}$.
∴当x=2m时,S最大值为$\frac{8}{3}$m2,
∵0<2<4,
∴最大透光面积能在自变量取值范围内取到.
点评 本题主要考查了二次函数的应用,根据矩形面积公式列出函数表达式是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在等腰△ABC和等腰△DEF中,∠A与∠D是顶角,下列判断不正确的是( )
| A. | ∠A=∠D时,两三角形相似 | B. | ∠A=∠E时,两三角形相似 | ||
| C. | ∠B=∠E时,两三角形相似 | D. | $\frac{AB}{BC}=\frac{DF}{EF}$时,两三角形相似 |
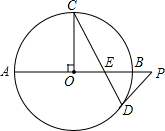 如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.
如图,AB是⊙O的直径,半径OC⊥AB,P是AB延长线上一点,PD切⊙O于点D,CD交AB于点E,判断△PDE的形状,并说明理由.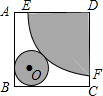 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r. 如图,在Rt△ABC中,∠ACB=90°,将其绕点A顺时针旋转80°得到△AB′C′,若∠B=30°,则∠CAB′为20°.
如图,在Rt△ABC中,∠ACB=90°,将其绕点A顺时针旋转80°得到△AB′C′,若∠B=30°,则∠CAB′为20°.