题目内容
3.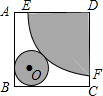 要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.
要按图所示的方式,剪裁边长为a正方形铁片,以扇形EDF为侧面、⊙O为底面制作圆锥模型.设DE=R,⊙O的半径为r.(1)写出R与r的关系;
(2)当a=5$\sqrt{2}$+2时,求r的值.
分析 (1)利用底面周长=展开图的弧长求出半径比;
(2)根据题意列方程$\sqrt{2}$r+r=$\sqrt{2}$a-R,$\sqrt{2}$r+r=$\sqrt{2}$a-4r,代入a的值即可得到结果.
解答 解:(1)利用底面周长=展开图的弧长可得;
2πr=$\frac{90πR}{180}$,
解得:R=4r;
(2)根据题意得:$\sqrt{2}$r+r=$\sqrt{2}$a-R,$\sqrt{2}$r+r=$\sqrt{2}$a-4r,
解得:r=$\frac{\sqrt{2}a}{5+\sqrt{2}}$,
当a=5$\sqrt{2}+$2时,r=2.
点评 本题考查了相切两圆的性质,列方程求未知数的值,关键是利用底面周长=展开图的弧长求得r与R的关系.

练习册系列答案
相关题目
13.下列各组数据分别是三角形三边长,是直角三角形的三边长的一组为( )
| A. | 5,6,7 | B. | 2,3,4 | C. | 8,15,17 | D. | 4,5,6 |
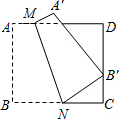 如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( )
如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的点B′处,点A的对应点为点A′,且B′C=3,则B′N的长是( ) 用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?
用8m长的铝合金型材做一个形状如图所示的矩形窗框,应做成长,宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?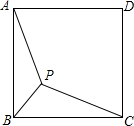 如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$.
如图,已知点P是正方形ABCD内的一点,连结PA、PB、PC.若PA=4,PB=2,∠APB=135°,则PC的长为2$\sqrt{6}$. 如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度.
如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度. 如图,⊙O与⊙O1交于A、B两点,O1点在⊙O上,AC是⊙O直径,AD是⊙O1直径,连结CD,求证:AC=CD.
如图,⊙O与⊙O1交于A、B两点,O1点在⊙O上,AC是⊙O直径,AD是⊙O1直径,连结CD,求证:AC=CD.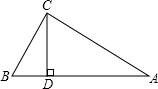 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.
如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.